Copyright © 1994 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1994. 32:
153-90 Copyright © 1994 by Annual Reviews. All rights reserved |
2.2. Equilibrium Nucleosynthesis
We have seen that the goal of any nucleosynthetic process is equilibrium. How does this goal vary with temperature? The answer is important because nature synthesizes nuclei at high temperature and ejects them into the medium between the stars at low temperature. If the nuclei stayed in equilibrium throughout this processing, we could use Equation (2) to determine the abundance of the various species. That the nuclei emerging from some nucleosynthetic process are not in general in an equilibrium distribution gives us important clues about how they were in fact made. We will turn to this point after discussing equilibrium nucleosynthesis in some detail.
Consider a system in NSE at some temperature. If the system expands adiabatically, the temperature will decrease. By Le Chatelier's Principle we know the system will respond to this stress by tending to counter it. How does the system do this? The answer is that nuclear reactions occur and release binding energy. This energy heats up the. system and tends to counter the temperature decrease from the expansion. Via these nuclear reactions, the system finds a new equilibrium if the reactions occur faster than the expansion.
As we have noted in Section 2.1, if
nuclear reactions assemble free
particles and light nuclei into heavier nuclei, there is a loss of
macroscopic states and a decrease in the entropy in baryons (free
nucleons and nuclei). The binding energy released in the reactions
goes into photons and leptons. This increases the numbers of
macroscopic states and, hence, the entropy in the photons and
leptons. We see that in building up the abundances of heavy nuclei, we
transfer entropy from the baryons to the photons and leptons. This is
apparent in Figure 3. Suppose a system at an
entropy per baryon of 10k begins in NSE at
T9 = 10(T9
 T/109K) and expands
adiabatically. The system cools. Because the system maintains
equilibrium, entropy leaves the baryons as the baryons assemble
themselves into heavier nuclei via nuclear reactions. This entropy
goes into the photons and leptons (electron-positron pairs).
T/109K) and expands
adiabatically. The system cools. Because the system maintains
equilibrium, entropy leaves the baryons as the baryons assemble
themselves into heavier nuclei via nuclear reactions. This entropy
goes into the photons and leptons (electron-positron pairs).
The entropy in baryons continues to fall until
T9  4. At this
point, the system has released essentially all its nuclear binding
energy. There is little further transfer of entropy from the baryons
to the other constituents of the system. We also note that beginning
around T9 = 4 the electron-positron pairs annihilate
into two photons. This transfers entropy from the e+ -
e- pairs into the
photons adiabatically. At late times, after the e+ -
e- pairs have
annihilated, the system is left with a residual abundance of electrons
to ensure charge neutrality. After the pairs have disappeared, the
system is a mix of relativistic photons and nonrelativistic nuclei and
electrons. Now for adiabatic expansion,
4. At this
point, the system has released essentially all its nuclear binding
energy. There is little further transfer of entropy from the baryons
to the other constituents of the system. We also note that beginning
around T9 = 4 the electron-positron pairs annihilate
into two photons. This transfers entropy from the e+ -
e- pairs into the
photons adiabatically. At late times, after the e+ -
e- pairs have
annihilated, the system is left with a residual abundance of electrons
to ensure charge neutrality. After the pairs have disappeared, the
system is a mix of relativistic photons and nonrelativistic nuclei and
electrons. Now for adiabatic expansion,

 T3
for relativistic particles and
T3
for relativistic particles and

 T3/2 for nonrelativistic particles. The
system at late times, because it is a mix of these two types of particles,
actually expands such that
T3/2 for nonrelativistic particles. The
system at late times, because it is a mix of these two types of particles,
actually expands such that

 Tb
where b is between 3/2 and 3. This
means that entropy now is transferred from the photons to the
translational entropy of the nonrelativistic particles. This is why
the entropy in photons declines after T9 = 1 and that
in leptons and baryons rises.
Tb
where b is between 3/2 and 3. This
means that entropy now is transferred from the photons to the
translational entropy of the nonrelativistic particles. This is why
the entropy in photons declines after T9 = 1 and that
in leptons and baryons rises.
What nuclei are made in such an expansion? Again we note that nuclear reactions tend to occur only if there is a release of binding energy to compensate for the loss of macroscopic states due to the decrease in the number of free particles. As our system expands and cools, the nuclei present in equilibrium will increase in mass. They will continue to increase in mass until they have reached the nuclide with the largest binding energy per nucleon. Once this nuclide dominates the abundance of nuclei, there is no further evolution in the abundances. This is because if the system attempts to arrange the nucleons into a more massive nucleus with a lower binding energy per nucleon, there will be a net decrease in the total binding energy of the system. Reactions giving this rearrangement of nucleons lead to a decrease in the number of free particles and in the energy available to the photons and leptons. There will thus be fewer ways to share the energy of the system and a decrease in the entropy. An expanding and cooling system can maintain NSE by driving the system to a composition dominated by the nuclear species with the largest binding energy per nucleon.
Figure 4 shows the mass fraction X(Z, A) = AY(Z, A) in NSE at temperatures T9 = 1 - 10 for an entropy per baryon of 10k and a net electron-to-baryon ratio Ye = 0.5. If we imagine the system begins at T9 = 10, alpha particles dominate the mass of the system. As the system expands and cools adiabatically, the abundances of heavier nuclei increase. At late times, however, all nucleons are locked up in 56Ni nuclei. This is because 56Ni has one proton for every two nucleons (Ye = 0.5), and it is the nucleus at Ye = 0.5 with the strongest binding energy per nucleon.
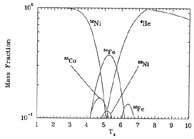
|
Figure 4. The mass fraction of species in NSE as a function of temperature for a system with entropy per baryon 10k Ye = 0.5. |
Figure 5 shows what happens if the entropy per baryon is 100k instead of 10k. Because of the larger entropy, the system has more free particles and tight nuclei at a given temperature. This is why free neutrons and protons dominate the abundances around T9 = 10 in Figure 5 while alpha particles dominate the abundances in Figure 4. We also see that alpha particle abundances build up only after T9 drops below 10 for entropy per baryon of 100k. As in the lower entropy case, however, the nucleons eventually end up all in 56Ni.
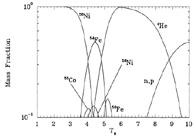
|
Figure 5. The mass fraction of species in NSE as a function of temperature for a system with entropy per baryon 100k and Ye = 0.5. |
What happens now if Ye is different from 0.5? Figure 6 shows what happens if the entropy per baryon is 10k and Ye = 0.4. Here there are six neutrons for every four protons. We see that the system at late times locks up all its nucleons into 56Ni. For Ye = 0.4, this is the nucleus with the largest binding energy per nucleon.
From Figure 6 we see that the final nucleus on which the system converges at low temperature is dependent on Ye because the final nuclei present must accommodate all of the neutrons and protons initially in the system. This final nucleus, however, is the nucleus with the largest binding energy for that Ye.
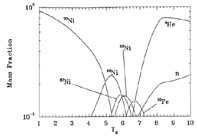
|
Figure 6. The mass fraction of species in NSE as a function of temperature for a system with entropy per baryon 10k and Ye = 0.4. |
Figure 7 gives an idea of what that nucleus is for Ye ranging from 0.35 to 0.6. In all cases, the nuclei are iron-group nuclei (Z = 26 - 34).
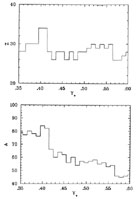
|
Figure 7. The proton number Z (top) and the mass number A (bottom) of the species with the largest binding energy per nucleon in each bin in Ye. Where experimental data are available, they are from Wapstra et al (1988). Where experimental data are unavailable, nuclear masses are from Möller & Nix (1988). |