Annu. Rev. Astron. Astrophys. 1994. 32: 153-90 Copyright © 1994 by Annual Reviews. All rights reserved

3.2. The Secondary r-Process

A system that does not achieve equilibrium may also produce r-process elements. As we have seen, as the bulk of the nuclei strive to reach the iron group, the reactions that carry them in this direction may release neutrons that then capture on pre-existing seed nuclei. If the number of neutrons released is sufficiently large, a solar system r-process abundance distribution may result. The nuclear reactions that would be the dominant producers of neutrons are (, n) reactions, and in particular the reactions ¹³C(, n)¹⁶O,²²Ne(, n)²⁵Mg, and ²⁵Mg(, n)²⁸Si.

A crucial feature of a secondary r-process is that it does not achieve (n,) - (, n) equilibrium. Such equilibrium occurs when the flows from (n, ) and (, n) reactions come into balance. The most abundant isotope of some element in such equilibrium is then the one for which the rate for that isotope (Z, A) to capture a neutron is equal to the rate for the resultant isotope (Z, A + 1) to suffer a disintegration (, n) reaction. The neutron-separation energy S_n, that is, the binding energy of the least tightly bound neutron, of this nucleus is, upon neglect of the A dependence of nuclear partition functions (e.g. Sato 1974, see also Howard et al 1993, and Meyer 1994),

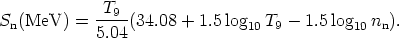
(5)

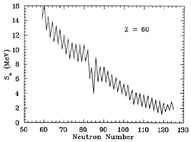
where n_n is the neutron number density in units of cm^-3. In secondary r-process sites, the neutron number density is typically ~ 10¹⁹ cm^-3 and T₉ ~ 1; thus, the dominant nuclei in (n, ) - (, n) equilibrium have S_n 3.0 MeV. Figure 8 shows the neutron-separation energies for the isotopes of neodymium (Z = 60). We see that the dominant isotope in (n, ) - (, n) equilibrium should be the one with neutron number N 110. The most neutron-rich beta-stable isotope of neodymium is ¹⁵⁰Nd (N = 90). The neutron sources in a secondary r-process would have to supply and maintain some 20 neutrons per seed nucleus in order to establish (n, ) - (, n) equilibrium. This is something they cannot do.

Figure 8. Neutron-separation energies for the isotopes of neodymium. The data are derived from Möller & Nix (1988).

Let us now consider possible secondary r-process sites. One possible site is the helium shell of an exploding massive star (Truran et al 1978, Thielemann et al 1979; see also Cowan et al 1980, 1983, 1985; Blake et al 1981; Klapdor et al 1981). As the supernova shock wave traverses this shell, it heats up the material to a temperature T₉ 1. Although this temperature is not high enough to force the material into NSE, it is high enough to drive material strongly in that direction. Among the main nuclear reactions that occur are (, n) reactions that liberate neutrons which can then capture on the pre-existing seed nuclei. Truran et al (1978) found that neutron captures could modify an s-process seed abundance distribution into an r-process distribution. Later work indicated that a seed distribution that is enhanced with respect to the solar system heavy-element distribution is required to produce the solar r-nuclei. Such an enhanced distribution could result from s-processing prior to shock passage if protons were to mix down into the helium shell to make ¹³C from the abundant ¹²C [via ¹²C(p, ) ¹³N(⁺)¹³C].It is apparent today, however, that the amount of ¹³C required is unrealistically large (Cowan et al 1985, Cameron et al 1985).

Lee et al (1979) considered supernova shock passage through the carbon shell. Here the ²²Ne(, )²⁵Mg reaction produces the neutrons. ²⁵Mg is also a neutron poison, however; it absorbs many of the liberated neutrons before they have a chance to capture on heavier seed nuclei. Wefel et al (1981) found that some heavy nuclei could be synthesized, but not the bulk of the r-nuclei.

Another intriguing secondary site is again the helium burning shell, but now the effects of neutrino inelastic scattering on ⁴He nuclei are included. The neutrinos come from the cooling nascent neutron star resulting from the core-collapse event. These neutrinos spall neutrons from the ⁴He (and other light) nuclei. The neutrons can then capture on the seed nuclei and drive an r-process (Epstein et al 1988). A detailed study of this "v-process" showed that some interesting nucleosynthesis may occur in such an event, but it could not have been a major contributor to the solar system r-process abundances (Woosley et al 1990).

All of the secondary r-process models studied to date have had profound difficulties which have rendered them implausible. Moreover, as shown in the next section, there are other reasons for favoring a primary over a secondary r-process. Nevertheless, the study of secondary r-process models has been valuable because they may have important applications to isotopic anomalies in meteorites (e.g. Clayton 1989, Howard et al 1992, Cameron et al 1993).