Annu. Rev. Astron. Astrophys. 1994. 32: 153-90 Copyright © 1994 by Annual Reviews. All rights reserved

4. THE s-PROCESS

Must we, as Solon advises, always keep the goal insight?

Aristotle, Nichomachean Ethics

The s-process is the other major nucleosynthetic process that assembles heavy elements. We know that the s-process path in the neutron number-proton number plane crosses the neutron closed shells at the valley of beta stability. This tells us that the s-process occurred in an environment with a much lower neutron density than the r-process. Also, the s-process occurred over a much longer time period.

In this section we seek to understand how the s-process occurs. We then turn to the question of s-process sites. Finally we consider constraints on those sites.

4.1. The s-Process Mechanism

Because of the neutron densities and timescales inferred for the s-process from the abundance peaks, we can infer that the s-process is not a freeze out from equilibrium. Instead, it is a neutron-capture process that occurs in a system striving to reach equilibrium, but falling short of its goal. The main reactions carrying the bulk of the nuclei towards the iron group can liberate neutrons. Pre-existing seed nuclei capture these neutrons and produce the s-nuclei. The s-process is clearly a secondary process.

The dominant reactions that can liberate neutrons are ¹³C(, n)¹⁶O and ²²Ne(, n)²⁵Mg. In these reactions, the neutron-rich isotopes, ¹³C and ²²Ne give up their excess neutrons to heavier nuclei. At this point, we may ask where these excess neutrons came from in the first place. The answer to this interesting question illustrates an important point about the overall nuclear evolution of the universe.

The abundances that emerge from the Big Bang are roughly 90% by number ¹H and 10% ⁴He (e.g. Walker et al 1991). This yields Y_e = 0.88. On the other hand, we may make the observation that ¹H and ⁴He are the only proton-rich (that is, with proton number greater than neutron number) stable isotopes in nature. This means that in order for nature to put the nucleons in the universe into nuclei with the strongest binding energy per nucleon (iron-group nuclei), the Y_e of the universe must decrease.

Most of the decrease in Y_e comes from the weak decays in the p - p chains and the CNO cycle during hydrogen burning. These interactions drop Y_e from 0.88 to 0.5 in material that has completed hydrogen burning. ⁴He itself does not have any excess neutrons, but some production of excess neutrons occurs in the CNO cycle due to reactions like ¹²C(p, ) ¹³N(⁺)¹³C. The net result is the conversion of a free proton into an excess neutron, and a drop in Y_e. The ²²Ne production builds up from abundant ¹⁴N produced in the CNO cycle. The sequence is ¹⁴N(, ) ¹⁸F(⁺) ¹⁸O(, ) ¹³Ne. Here it is the fact that the only stable isotope of flourine is neutron rich that leads to a decrease in Y_e. We see that the excess neutrons in ¹³C and ²²Ne are a consequence of the overall drive to decrease Y_e in stars. We must keep the goal of the nuclei in sight to understand where the excess neutrons come from that drive the s-process.

The first attempts to understand the details of the s-process led to the classical model. The neutron density is always low in the s-process (compared to the r-process). If a nucleus is unstable to ^- decay following neutron capture in the s-process, it will almost always ^- decay to the first available stable isobar before it can capture another neutron. Thus, it generally suffices in s-process studies to follow only the abundances as a function of mass number, which only change by neutron capture. In this approximation, the rate of change of the abundance N_A of nuclei with mass number A is

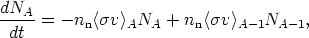
(9)

where n_n is the neutron number density and <v>_A is the thermally averaged neutron-capture cross section for the stable isobar of mass number A. We can write <v>_A as _A v_T, where v_T is the thermal velocity of neutrons and _A is an average cross section, given in terms of v_T. With the definition of the neutron exposure

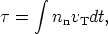
(10)

we find

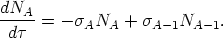
(11)

Note that the neutron exposure is a fluence. It has units of inverse millibarns (1 barn = 10^-24 cm²). Because it is a neutron flux integrated overtime, it is an appropriate evolutionary parameter for the s-process. If the s-process achieves a steady state, then dN_A / d 0 and _A N_A constant.

Clayton et al (1961) were able to show that a single neutron exposure r could not reproduce the solar system's abundance of s-only nuclei. Seeger et al (1965) showed that an exponential distribution of exposures, given by

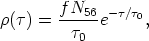
(12)

where f is a constant and N₅₆ is the initial abundance of ⁵⁶Fe seed, did reproduce the solar distribution of s-nuclei. For the distribution of exposures given in Equation (12), Clayton & Ward (1974) found that for an exponential average of flows in the s-process

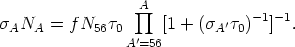
(13)

A fit to the empirical _A N_A for s-only nuclei then gives the quantities f and .

A complication to the above classical model is the branching that occurs at certain isotopes. Here it may be that the ^- decay rate is not considerably greater than the neutron-capture rate. In some cases the nucleus may ^- decay before neutron capture and in others it may neutron capture before suffering ^- decay. The assumptions leading to Equation (9) thus break down. Ward et al (1976) developed an analytic treatment of branching in the case of a time-independent neutron flux. For time-dependent neutron fluxes, it is necessary in general to solve a full network of nuclei numerically (e.g. Howard et al 1986). Since the s-process branchings will in general be temperature and neutron density dependent, s-nuclei branchings are important diagnostics of the environment in which the s-process occurred. We will see this in more detail in Section 4.3.