This modified dynamics, MOND, introduces a constant with the dimensions of an acceleration, 0, and posits that standard Newtonian dynamics is a good approximation only for accelerations that are much larger than 0. The exact behavior in the opposite limit is described by the specific underlying theory, to be described below. However, the basic point of MOND, from which follow most of the main predictions, can be simply put as follows: a test particle at a distance r from a large mass M is subject to the acceleration a given by
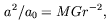
| (1) |
when a << a0, instead of the standard expression a = MGr-2, which holds when a >> a0. The two expressions may be interpolated to give the heuristic relation
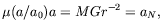
| (2) |
where aN is the Newtonian expression for the acceleration,
and the interpolating function µ(x) satisfies
µ(x)
1 when x
>> 1, and
µ(x)
x when x << 1. This expression, while lacking from
the formal point of view,
is very transparent, and captures the essence of MOND. I shall
describe below more presentable theories based on this basic
relation, but these are still phenomenological theories into
which the form of µ(x) has to be put in by hand. It will
hopefully follow one day from a more basic
underlying theory for MOND, which we still lack. Most of the
implications of MOND do not depend strongly on
the exact form of µ. Much of the phenomenology pertinent to
the mass discrepancy in galactic systems occurs in the deep-MOND
regime (a << a0), anyway, where we know that
µ(x)
x.