


Because MOND revolves around acceleration, which is so much in the heart of inertia, one is directed, with the above imagery in mind, to consider that inertia itself, not just MOND, is a derived concept reflecting the interactions of bodies with some agent in the background. The idea, which is as old as Newton's second law, is the basic premise of the Mach's principle. The great sense that this idea makes has lead many to attempt its implementation. The agent responsible for inertia had been taken to be the totality of matter in the Universe.
Arguably, an even better candidate for the inertia-producing agent, which I have been considering since the early 1990s, in the hope of understanding MOND's origin, is the vacuum. The vacuum is known to be implicated in producing or modifying inertia; for example, through mass renormalization effects, and through its contribution to the free Maxwell action in the form of the Euler-Heisenberg action [Itzykson & Zuber 1980]. Another type of vacuum contributions to inertia have been discussed by [Jaekel & Reynaud 1993]. But, it remains moot whether the vacuum can be fully responsible for inertia.
The vacuum is thought to be Lorentz invariant, and so indifferent to
motion with constant speed. But acceleration is another matter. As
shown by Unruh in the 1970s, an accelerated body is alive to its
acceleration with respect to the vacuum, since it finds itself
immersed in a telltale radiation, a transmogrification of the
vacuum that reflects his accelerated motion. For an observer on a
constant-acceleration (a) trajectory this radiation is thermal,
with T =  a, where
a, where


 /
2
/
2 kc. The effect
has been also calculated approximately for highly relativistic
circular motions; the spectrum is then not exactly thermal. In
general, it is expected that the effect is non-local; i.e.,
depends on the full trajectory.
kc. The effect
has been also calculated approximately for highly relativistic
circular motions; the spectrum is then not exactly thermal. In
general, it is expected that the effect is non-local; i.e.,
depends on the full trajectory.
Unruh's result shows that the vacuum can serve as an inertial frame. But
this is only the first step. The remaining big question is how
exactly the vacuum might endow bodies with inertia. At any rate,
what we want is the full MOND law of inertia, with the transition
occurring at accelerations of order a0 that is related to
cosmology. We then have to examine the vacuum in the context of
cosmology. How it affects, and is being affected by, cosmology.
One possible way in which cosmology might enter is through the
Gibbons-Hawking effect, whereby even inertial observers in an
expanding universe find themselves embedded in a palpable
radiation field that is an incarnation of the vacuum. The problem
has been solved for de Sitter Universe, which is characterized by
a single constant: the cosmological constant,
 , which is
also the square of the (time independent) Hubble constant. In this
case the spectrum is also thermal with a temperature
T =
, which is
also the square of the (time independent) Hubble constant. In this
case the spectrum is also thermal with a temperature
T =  c(
c( /
3)1/2.
/
3)1/2.
In the context of MOND it is interesting to know what sort of
radiation an observer sees, who is accelerated in a non-trivial
universe: If the Unruh temperature is related to inertia, then it
might be revealing to learn how this temperature is affected by
cosmology. This can be gotten for the case of a
constant-acceleration observer in a de Sitter Universe. For this
case the radiation is thermal with a temperature T =
 (a2 +
c2
(a2 +
c2
 / 3)1/2
[Deser & Levin
1997].
Inertia, which is
related to the departure of the trajectory from that of an
inertial observer, who in de Sitter space sees a temperature
/ 3)1/2
[Deser & Levin
1997].
Inertia, which is
related to the departure of the trajectory from that of an
inertial observer, who in de Sitter space sees a temperature
 c(
c( /
3)1/2, might be proportional to the temperature difference
/
3)1/2, might be proportional to the temperature difference
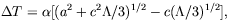
| (12) |
and this behaves exactly as MOND inertia should:
it is proportional to a for
a > > a0
 2c(
2c( /
3)1/2, and to a2 /
a0 for a < < a0; and,
we reproduce the connection of
a0 with cosmology. Of course, in the modified-inertia
paradigm
this would reflect on a "linear", constant-acceleration motion,
while circular trajectories will probably behave differently. But
the emergence of an expression a-la MOND in this connection
with the vacuum is very interesting.
/
3)1/2, and to a2 /
a0 for a < < a0; and,
we reproduce the connection of
a0 with cosmology. Of course, in the modified-inertia
paradigm
this would reflect on a "linear", constant-acceleration motion,
while circular trajectories will probably behave differently. But
the emergence of an expression a-la MOND in this connection
with the vacuum is very interesting.