Usually it is a matter of taste what physical quantity is
chosen as 
. For example, in
a lifetime experiment some workers would solve for the lifetime,
*, while others would solve for
*, where
=
1/. Some workers prefer to use
momentum, and
others energy, etc. Consider the case of two related physical
parameters and
. The maximum-likelihood
solution for is
obtained from the equation
ðw / ð = 0. The
maximum-likelihood
solution for is obtained
from
ðw / ð =
0. But then we have
|
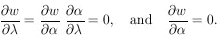
Thus the condition for the maximum-likelihood solution is
unique and independent of the arbitrariness involved in choice
of physical parameter. A lifetime result
* would be related
to the solution
* by
* =
1/*.
The basic shortcoming of the maximum-likelihood method is
what to do about the prior probability of
. If the prior
probability of is
G() and the
likelihood function obtained for the experiment alone is
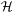(), then the joint likelihood
function is
|
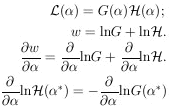
give the maximum-likelihood solution. In the absence of any
prior knowledge the term on the right-hand side is zero. In
other words, the standard procedure in the absence of any prior
information is to use a prior distribution in which all values
of are equally
probable. Strictly speaking, it is impossible
to know a "true" G(),
because it in turn must depend on its
own prior probability. However, the above equation is useful
when G() is the
combined likelihood function of all previous experiments and
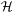() is the likelihood function of
the experiment under consideration.
There is a class of problems in which one wishes to determine
an unknown distribution in
,
G(), rather than a single
value . For example, one may
wish to determine the momentum
distribution of cosmic ray muons. Here one observes
|
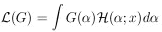
where 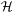(; x) is known from the
nature of the experiment and
G() is the function to be
determined. This type of problem is discussed in Reference 5.