A common type of problem which falls into this category
is the determination of a cross section or a mean free path.
For a mean free path 
, the
probability of getting an event
in an interval dx is
dx / . Let
P(0, x) be the probability of
getting no events in a length x. Then we have
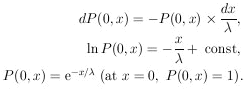
| (19) |
Let P(N, x) be the probability of finding N events in a length x. An element of this probability is the joint probability of N events at dx1, ..., dxN times the probability of no events in the remaining length:
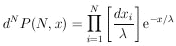
| (20) |
The entire probability is obtained by integrating over the N-dimensional space. Note that the integral
|
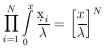
does the job except that the particular probability element in Eq. (20) is swept through N! times. Dividing by N! gives
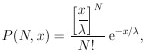
| the Poisson distribution | (21) |
As a check, note
|
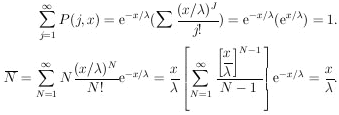
Likewise it can be shown that
= 
.
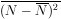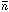Equation (21) is often expressed in terms of
:
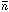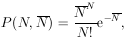
| the Poisson distribution | (22) |
This form is useful in analyzing counting experiments. Then
the "true" counting rate is
.
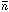We now consider the case in which, in a certain experiment,
N events were observed. The problem is to determine the
maximum-likelihood solution for
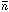and its
error:
|
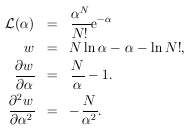
Thus we have
|
and by Eq. (7),
|
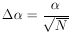
In a cross-section determination, we have
=
x
,
where is
the number of target nuclei per cm3 and x is the total
path length. Then
|
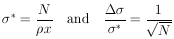
In conclusion we note that
:
|
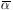
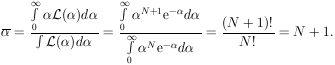