An important job for a physicist who plans new experiments is to estimate beforehand just how many events will be needed to "prove" a certain hypothesis. The usual procedure is to calculate the average logarithm of the likelihood ratio. The average logarithm is better behaved mathematically than the average of the ratio itself. We have
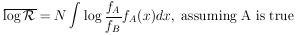
| (32) |
or
|
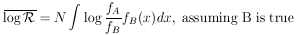
Consider the example (given in Section 3) of the K+ meson. We believe spin zero is true, and we wish to establish betting odds of 104 to 1 against spin 1. How many events will be needed for this? In this case Eq. (32) gives
|
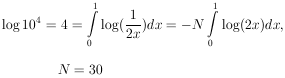
Thus about 30 events would be needed on the average. However,
if one is lucky, one might not need so many events. Consider
the extreme case of just one event with
x = 0 : 
would then
be infinite and this one single event would be complete proof
in itself that the K+ is spin zero. The fluctuation (rms
spread) of log 
for a
given N is
|
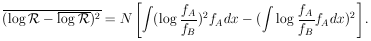