APPENDIX III. LEAST SQUARES WITH ERRORS IN BOTH VARIABLES

Experiments in physics designed to determine parameters in the functional relationship between quantities x and y involve a series of measurements of x and the corresponding y. In many cases not only are there measurement errors y_i for each y_j, but also measurement errors x_j for each x_j. Most physicists treat the problem as if all the x_j = 0 using the standard least squares method. Such a procedure loses accuracy in the determination of the unknown parameters contained in the function y = f (x) and it gives estimates of errors which are smaller than the true errors.

The standard least squares method of Section 15 should be used only when all the x_j << y_i. Otherwise one must replace the weighting factors 1 / _i² in Eq. (24) with (_j)^-2 where

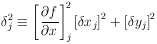
(36)

Eq. (24) then becomes

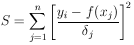
(37)

A proof is given in Ref. 7.

We see that the standard least squares computer programs may still be used. In the case where y = ₁ + ₂x one may use what are called linear regression programs, and where y is a polynomial in x one may use multiple polynomial regression programs. The usual procedure is to guess starting values for ðf / ð x and then solve for the parameters _j* using Eq. (30) with _j replaced by _j. Then new [ðf / ð x]_j can be evaluated and the procedure repeated. Usually only two iterations are necessary. The effective variance method is exact in the limit that ðf / ð x is constant over the region x_j. This means it is always exact for linear regressions.