When M parameters are to be determined from a single experiment
containing N events, the error formulas of the preceding
section are applicable only in the rare case in which the errors
are uncorrelated.. Errors are uncorrelated only for
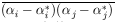= 0 for all
cases with
i 
j. For the
general case we Taylor-expand
w(
) about
(*):
|
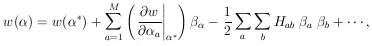
where
|
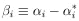
and
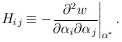
| (9) |
The second term of the expansion vanishes because
ðw / ð = 0
are the equations for *
|
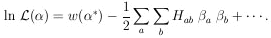
Neglecting the higher-order terms, we have
|
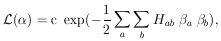
(an M-dimensional Gaussian surface). As before, our error
formulas depend on the approximation that
() is
Gaussian-like in the region
i
i*. As mentioned in
Section 4, if the
statistics are so poor that this is a poor approximation, then
one should merely present a plot of
(). (see Appendix IV).
According to Eq. (9), H is a symmetric matrix. Let U be the unitary matrix that diagonalizes H:
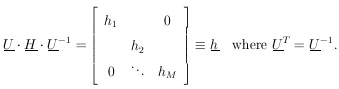
| (10) |
Let
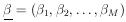and
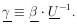. The
element of
probability in the 
-space is
|
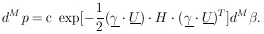
Since
|U| = 1 is the Jacobian relating the volume elements
dM and
dM
, we have
|
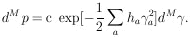
Now that the general M-dimensional Gaussian surface has been put in the form of the product of independent one-dimensional Gaussians we have
|
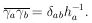
Then
|
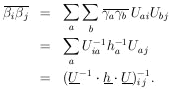
According to Eq. (10), H = U-1 . h . U, so that the final result is
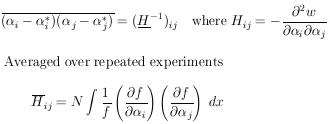
| Maximum Likelihood Errors, M parameters (11) |
(A rule for calculating the inverse matrix H-1 is
|
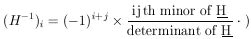
If we use the alternate notation V for the error matrix H-1, then whenever H appears, it must be replaced with V-1; i.e., the likelihood function is
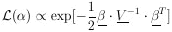
| (11a) |
Example 2
Assume that the ranges of monoenergetic particles are
Gaussian-distributed with mean range
1 and straggling
coefficient
2 (the standard
deviation). N particles having ranges
x1,..., xN are observed. Find
1*,
2*, and their
errors . Then
|
|
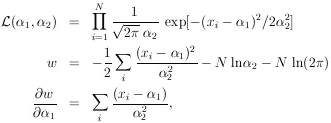
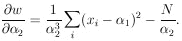
The maximum-likelihood solution is obtained by setting the above two equations equal to zero.
|
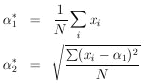
The reader may remember a standard-deviation formula in which N is replaced by (N - 1):
|
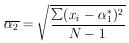
This is because in this case the most probable value,
2*, and
the mean,
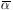2 ,
do not occur at the same place. Mean
values of
such quantities are studied in Section 16.
The matrix H is
obtained by evaluating the following quantities at
1* and
2*:
|
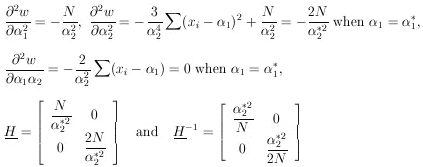
According to Eq. (11), the errors on
1 and
2 are the
square
roots of the diagonal elements of the error matrix, H-1:
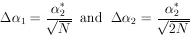
| (this is sometimes
called the error of the error). |
We note that the error of the mean is
1/sqrt[N]
where
=
2 is
the standard deviation. The error on the determination of
is
/sqrt[2N].
Correlated Errors
The matrix
Vij 
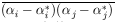is
defined as the error matrix (also called the covariance matrix of
). In Eq. 11
we have shown that
V = H-1 where
Hij = - ð2 w /
(ði
ðj). The
diagonal elements of V are the variances of the
's. If all the
off-diagonal elements are zero, the errors in
are uncorrelated
as in Example 2. In this case contours of constant w plotted
in (1,
2) space would be
ellipses as shown in Fig. 2a. The
errors in 1 and
2 would be the
semi-major axes of the contour ellipse where w has dropped by
½ unit from its maximum-likelihood
value. Only in the case of uncorrelated errors is the rms error
j =
(Hjj)-½ and then there is no
need to perform a matrix inversion.
|
Figure 2. Contours of constant w as
a function of |
In the more common situation there will be one or more
off-diagonal elements to
H and the errors are correlated
(V has
off-diagonal elements). In this case (Fig. 2b)
the contour ellipses are inclined to the
1,
2 axes. The rms
spread of 1
is still 1 =
sqrt[V11], but it is the extreme limit of
the ellipse projected on the
1-axis. (The
ellipse "halfwidth" axis is
(H11)-½ which is smaller.) In cases
where Eq. 11 cannot be evaluated analytically, the
*'s can be found numerically and
the errors in can be found
by Plotting the ellipsoid where
w is 1/2 unit less than w * . The
extremums of this ellipsoid are
the rms error in the 's. One
should allow all the
j to change
freely and search for the maximum change in
i which makes
w = (w * - ½). This maximum
change in
i, is the
error in i and is
sqrt[V11].