Annu. Rev. Astron. Astrophys. 1993. 31: 689-716 Copyright © 1993 by Annual Reviews. All rights reserved

2. THE CDM SCENARIO DEFINED

2.1. History: Origin of the Standard Model

Starting with Zwicky's (1933) determination of the mass in clusters of galaxies, there have been many independent lines of evidence which have argued that the dynamically detected mass density of the universe [in units of the critical density (8 / 3) G _crit H² (h × 100 km s^-1)²] is larger than what we can easily account for in stars and gas with "normal" mass-to-light ratios assumed. Dynamical studies of galaxy rotation curves, galaxy groups (e.g. Nolthenius & White 1987), and clusters give _d (0.1-0.2) with Peebles (1986) giving a slightly higher value (_d 0.3) and some recent work indicating values approaching unity. However, the corresponding value for stars has been estimated, from the observed light density of the universe, as _* 0.003(M/L/5)h^-1. This large discrepancy led to the concept of "dark matter" and the hope that the theoretically attractive value of = 1 could be valid. To achieve a flat cosmology by this means, of course, would require that most of our dynamical estimates be wrong by a factor of 5-10 and that, furthermore, most of the dark matter would need to be of a non-baryonic nature, since light element nucleosynthesis calculations typically give _b 0.013 h^-2 (Walker et al 1991), which is even smaller than our dynamical measures.

To resolve this issue by a simple stroke of assumption, theoreticians have postulated the existence of some form of exotic matter which, when added to the baryonic component, would produce a flat ( = 0) cosmology:

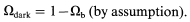
(1)

The fact that we have not detected this matter requires that it must interact very weakly with normal matter, and the fact that it does not show up in our dynamical estimates requires that it be less clustered than our usual dynamical probes, i.e. galaxies.

Dark matter has advantages as well in understanding the origin of perturbations in the universe. One imagines that, at early times, there were adiabatic fluctuations in the dark matter fluid, the radiation fluid, and in ordinary matter. It is most natural and simple to assume adiabatic fluctuations and a power spectrum such that (M / M)_rms on the scale of the horizon is a fixed (small) number at early times. This implies that, at any given time, |(k)|² k¹, where (k) is the Fourier amplitude of the density power spectrum at that time and k is the wave number. The assumed initial power spectrum, named after its independent originators Harrison-Zeldovich-Peebles ("HZP"), is normally taken as standard in the CDM picture, although variants have been discussed. Further, it is assumed that the phases of different, independent modes are uncorrelated and that the amplitudes have a Gaussian distribution about the mean. Perturbations with wavelengths smaller than the horizon grow very slowly during the era of radiation domination, but after z_eq = 2.5 × 10⁴ h², the dark matter density dominates over that of massless particles, and it is by hypothesis "cold," nonrelativistic, at this time when the mass within the horizon is ~ 10¹⁵ M. For very long wavelengths, the power spectrum P(k) maintains its initial form P(k) k; these long wavelengths have always grown at the kinematic rate appropriate for wavelengths larger than the horizon. Dark matter fluctuations on scales smaller than the horizon at decoupling have grown relatively less, with (asymptotically) P_k k^-3 for k (cf Figure 1).

Figure 1. (a) Power spectra for fluctuations in density ( / ) at redshift zero for the cold dark matter scenario, and variants, all normalized so that 8 (M / M)rms on the 8h-1 scale is unity. Note that both open and tilted variants have relatively more large-scale power (to small-scale power) as compared to the standard model. (b) Standard CDM spectrum at redshift zero analyzed with the matched filter (Babul 1989) [as opposed to the top-hat filter used in (a)] which picks out objects of the stated mass. Note that, for models with reheating to 104 K, fluctuations on mass scales smaller than 109 M are suppressed.

The third apparent advantage of the CDM scenario is that the characteristic length seems appropriate to making the structures that we have observed. This is best seen if we filter the power spectrum with the "matched filter" Babul (1990) designed to pick out structures of a given length or mass scale. The normally used Gaussian or top-hat filters look for all structures on scales larger than or equal to a given scale and, since they show the integral, can give a false impression of small-scale power. Figure 1b (Babul 1989, 1990) shows that, if the gas is never "refrigerated" (i.e. colder than T_CBR), then the peak is at 10⁵ M and scales with M < 10², never become nonlinear. And, if the gas is reheated to 10,000 K, then all mass scales less than ~ 10⁹ M are stable.

Among the first to propose the CDM scenario and to calculate the dark matter power spectrum were Peebles (1982), Primack & Blumenthal (1983), and Bond & Efstathiou (1984). Combining the CDM power spectrum with simplified ideas of gas cooling (Rees & Ostriker 1977, Silk 1977, Binney 1977), various groups of authors, for example Blumenthal et al (1984, 1985), were able to put together a plausible picture of galaxy formation in the CDM scenario. On larger scales, the numerical N-body simulations of Davis, Frenk, Efstathiou, White, and others (see Frenk 1991 for detailed references) based on the CDM initial power spectrum showed considerable success in reproducing observed structures. But the real universe of galaxies tended to be more clumped than the simulations, so a concept of "bias" was invented with "b" defined as the ratio of (observable) galaxy fluctuations, to the more fundamental mass fluctuations:

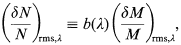
(2)

where we have allowed bias to be a function of scale. Kaiser (1984) provided a simple and elegant statistical explanation for the origin of bias; among others, Dekel & Rees (1987) described physical mechanisms by which bias could arise; and White et al (1987) showed how bias could operate in the CDM scenario. The concept of bias also could be used to solve another problem: The apparent defect in observed dynamical mass density compared to the assumed critical value required for a flat K = 0 model could hopefully be understood if the tracer galaxies were more clustered than the underlying mass distribution. And, since the increase in typically goes as b^5/3, a moderate value of b sufficed to bring dynamical observations into accord with the theoretical prejudice.

Thus, the CDM scenario seemed to explain and reproduce many important features of the universe. A natural origin for fluctuations was proposed in inflationary scenarios as well as an efficient way for these to grow undetected at early epochs. It seemed that the spectrum of perturbations had the right shape to explain galaxy formation in terms of both an appropriate epoch and an appropriate mass distribution. Additionally, numerical simulations produced structures on large scales which, if an appropriate bias was assumed, seemed reasonably similar to observed large-scale structure. Finally, a bias of the same type could self-consistently reconcile a small value for _dyn observed with the larger value of ₀ = 1 assumed. There was great optimism in the community of theoretical astrophysics over these results, and CDM became the reigning paradigm, with numerous papers, conferences, symposia, etc devoted to elaborating this model.