Copyright © 1993 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1993. 31:
689-716 Copyright © 1993 by Annual Reviews. All rights reserved |
2.3. Galaxy Formation and Bias
However, most of the work performed to date has followed only the dynamically dominant component - the collisionless dark matter. The pioneering work was performed by M. Davis, G. Efstathiou, C. Frenk, and S. D. M. White ("DEFW" in numerous combinations, e.g. 1985), with recent very large-scale simulations by Bertschinger & Gelb (1991) and Park & Gott (1991). Here one follows dark matter particles on their trajectories and then groups them according to various algorithms into "halos" within which one assumes that the baryonic galaxies would be embedded. A mass function for these dark matter halos can be constructed, and it is plausibly like that which is inferred from dynamical measurements to be characteristic of normal galaxies (cf Figure 2). One can then investigate the properties and the spatial distribution of these halos and compare these to the developing observations of the spatial and velocity distributions seen within and among nearby galaxies (Frenk et al 1988, Dubinski & Carlberg 1991, Warren et al 1992).

|
Figure 2. (a) Mass distribution of
dark matter halos in the biased
( |
But, how is the association to be made? On physical grounds, it seems plausible that gas is turned more efficiently into stars in regions where the density is large and cooling is efficient. Primack et al (1983; cf also White & Rees 1978, White & Frenk 1991, and Baron & White 1987, for galaxy formation in a CDM universe) were able to combine the CDM spectrum with physical arguments to show that the properties of normal spiral and elliptical galaxies could reasonably have been expected to be produced by cooling assemblages of baryons accumulating in the potential wells of the dark halos.
But, more typically, those wishing to compare the theoretical
simulations with observations simply defined a quantity "bias"
( b) which
expressed the ratio of galaxy-to-mass fluctuations (Equation 2). With
(
b) which
expressed the ratio of galaxy-to-mass fluctuations (Equation 2). With
( M/M) computed
and b (> 1) estimated,
(
M/M) computed
and b (> 1) estimated,
( N/N) was
derivable. Equation 2 is implicitly a function of scale or wave number
k, so in principle one
may expect that the bias b should also be a function of scale
with larger
values appropriate to small scales where cooling will be more efficient.
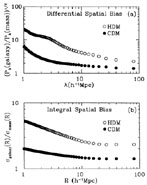
Figure 3 presents bias as a function of scale
from a recent detailed hydrodynamic simulation of
Cen & Ostriker (1992b).
N/N) was
derivable. Equation 2 is implicitly a function of scale or wave number
k, so in principle one
may expect that the bias b should also be a function of scale
with larger
values appropriate to small scales where cooling will be more efficient.
Figure 3 presents bias as a function of scale
from a recent detailed hydrodynamic simulation of
Cen & Ostriker (1992b).
|
Figure 3. Spatial bias (open circles - HDM and closed circles - CDM) from Cen & Ostriker (1992b) hydrodynamic simulation. (a) Differential bias, the simple ratio of the amplitudes of the power spectra of the galaxy and dark matter components. (b) Bias on a top-hat window of radius Rh-1 Mpc. On the standard 8 h-1 Mpc scale, the integral bias is 1.6. |