


After emission-line variability was detected, it became clear to a number of investigators 5, 23, 7, 10, 3 that the kinematics and the geometry of the BLR can be tightly constrained by characterizing the emission-line response to continuum variations. The time delay between continuum and emission-line variations are ascribed to light travel-time effects within the BLR; the emission lines "echo" or "reverberate" to the continuum changes. The Blandford & McKee paper 7, regarded as the seminal paper in the field, first introduced the term "reverberation mapping" to describe this process. Reviews of progress in reverberation mapping are provided by Peterson62 and Netzer & Peterson 58.
Because the emission lines vary with the UV/optical continuum (with some small time delay), we can immediately draw several important conclusions:
 < 912 Å,
h
< 912 Å,
h
 13.6 eV).
13.6 eV).
This information provides the crucial underpinning for the assumptions detailed below. But before we proceed any further, we need to remind ourselves of some of the basic characteristics of the line-emitting gas, much of which we derive by comparing the observed line spectra with the predictions of photoionization equilibrium computer codes (see the contribution by Netzer for a more complete discussion). In general, photoionization equilibrium models of the line-emitting clouds are parameterized by the shape of the ionizing continuum, elemental abundances, and an "ionization parameter"
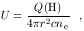
| (13) |
where

| (14) |
is the number of hydrogen-ionizing
(h 1 = 13.6 eV)
photons emitted per second by the central source.
1 = 13.6 eV)
photons emitted per second by the central source.
Essentially, U characterizes the ionization balance within the cloud, as Q(H) / r2 is proportional to the number of photoionizations occurring per second at the incident face of the cloud, and ne is proportional to the recombination rate. For a typical Seyfert 1 galaxy (NGC 5548)
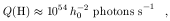
| (15) |
where h0 is the Hubble constant in units of 100 km
s-1 Mpc-1.
By taking the electron density to be ne
 1011 cm-3 and the distance to the central source to be
10 light days, we find U
1011 cm-3 and the distance to the central source to be
10 light days, we find U
 0.1.
The line-emitting clouds are ionized to the
"Strömgren depth" ,
0.1.
The line-emitting clouds are ionized to the
"Strömgren depth" ,
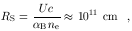
| (16) |
at which point virtually all of the incident ionizing
photons have been absorbed. In BLR clouds,
the region beyond the Strömgren zone is
partially ionized, n(H+)
 0.1n(H0),
and heated primarily by far infrared radiation
24
and partly by high-energy X-rays
45.
In Eq. (16),
0.1n(H0),
and heated primarily by far infrared radiation
24
and partly by high-energy X-rays
45.
In Eq. (16),
 B is the
Menzel-Baker case B recombination coefficient
59.
B is the
Menzel-Baker case B recombination coefficient
59.