


3.2. The Transfer Equation
Under these assumptions, the relationship between the continuum and emission lines can be written in terms of the "transfer equation",
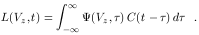
| (20) |
Here C(t) is the continuum light curve,
L(Vz, t) is the emission-line flux at
line-of-sight velocity Vz and time t,
and 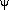 (Vz,
(Vz,
 ) is
the "transfer function" at Vz and time delay
) is
the "transfer function" at Vz and time delay
 .
Inspection of the transfer equation
shows that the transfer function is simply the time-smeared emission-line
response to a
.
Inspection of the transfer equation
shows that the transfer function is simply the time-smeared emission-line
response to a  -function
outburst in the continuum. Note that
causality requires that the lower limit on the integral is
-function
outburst in the continuum. Note that
causality requires that the lower limit on the integral is
 = 0.
= 0.
Solution of the transfer equation to obtain the transfer function is a classical inversion problem in theoretical physics: the transfer function is essentially the Green's function for the system. Unfortunately, it is difficult to find a stable solution to such equations, especially when the data are noisy and sparse, as they usually are in astronomical applications.
In practice, most analyses have concentrated on solving the velocity-independent (or 1-d) transfer equation,
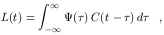
| (21) |
where both 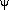 (
( ) and L(t) represent integrals
over the emission-line width.
) and L(t) represent integrals
over the emission-line width.
The transfer equation is a linear equation. In reality, however,
the relationship between the observed continuum and the emission-line
response is likely to be nonlinear. We therefore approximate
C(t) = 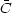 +
+
 C and
L(t) =
C and
L(t) = 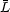 +
+
 L, where
L, where
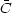 and
and
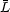 represent constants, usually the mean value of the
continuum and line flux, respectively. We can then treat
deviations from the mean as linear perturbations and
the equation we actually solve is
represent constants, usually the mean value of the
continuum and line flux, respectively. We can then treat
deviations from the mean as linear perturbations and
the equation we actually solve is
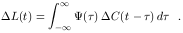
| (22) |
Most existing data sets are inadequate for transfer-function solution, and simpler analyses are used. The most commonly used tool in analysis of AGN variability is cross-correlation, which will be discussed in detail in Sec. 4.