Annu. Rev. Astron. Astrophys. 1998. 36: 267-316 Copyright © 1998 by Annual Reviews. All rights reserved

3. OBSERVATIONAL RESULTS

3.1. Redshift Evolution of the Lyman Alpha Forest

In an individual QSO line of sight, observations of the high redshift (z ~ 3) Ly forest can extend over a redshift range z greater than unity. Then we are sampling a significant fraction of a Hubble time, and it is natural to expect to see changes in the absorption pattern, e.g., in the rate of incidence of absorption lines with redshift, or in the mean optical depth.

EVOLUTION OF THE LINE DENSITY     An analytic expression (Wagoner 1967, Bahcall & Peebles 1969) can be given for the number of absorption systems per unit redshift, d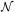 / dz, in terms of the comoving number density n₀(z) of absorbers, the geometric absorption cross section (z), and the Hubble constant H₀:

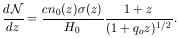
(6)

For absorbers with no intrinsic evolution,

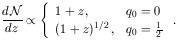
(7)

The transformation from redshift z to the coordinate X(z) = ₀^z(1 + z)^-1 (1 + 2q₀z)^1/2 dz (Wagoner 1967) is sometimes used to take out the mere cosmological redshift dependence, such that d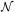 / dX = cn₀(z) (z) H₀^-1.

Peterson (1978) first pointed out an increase in the number of Ly clouds with redshift beyond what was expected for a populations of non-evolving objects. At first this result was subject to some debate (see the summary by Murdoch et al. 1986), but it is now clear that the Ly forest as a whole evolves quite strongly with z. The observationally determined evolution in the number of absorbers above a certain column density threshold is usually expressed in the form

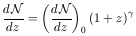
(8)

(Sargent et al 1980; Young et al 1982b), where the exponent includes the cosmological dependence. Much observational effort has been devoted to studying the redshift number density evolution, but unfortunately the resulting conclusions are far from robust. This is because Ly cloud column densities N are distributed according to a power law N ^- with index ~ 1.5 (see below) so the majority of lines in any column density limited sample are always close to the threshold, and small variations in imposing the threshold can cause large changes in the estimated numbers of lines, and in . Moreover, line blending, and its dependence on spectral resolution, data quality, and redshift can make a large difference in the normalization (d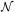 / dz)₀, with individual studies differing by a factor of two or more (the interested reader may refer to Parnell & Carswell 1988; Liu & Jones 1988; Trevese et al 1992, and Kim et al 1997 for a discussion of blending effects). Each individual study has a finite redshift range available so that the uncertainty in the normalization is correlated with the exponent ; the differences between the observed values of exhibit a disturbingly large scatter. Thus the line counting approach is unsatisfactory when it comes to redshift evolution. Rather than discussing the many individual (and sometimes mutually inconsistent) contributions made to this question we will outline some typical results as follows.

At lower resolution (FWHM ~ 50-100 kms^-1) large samples of lines have been used to investigate this topic. The values tend to lie between the low value = 1.89 ± 0.28 obtained by Bechtold (1994), (W > 0.32 Å), and the high one = 2.75 ± 0.29 (for W > 0.36 Å) from the study by Lu et al (1991). High resolution spectra, usually confined to z > 2, tend to give an equally wide range of values: = 1.7 ± 1.0 (W > 0.2 Å; Atwood et al 1985); 2.9 ± 0.3 (2 < z < 4.5; Cooke et al. 1997); = 2.78 ± 0.71 (logN > 13.77; 2 < z < 3.5; Kim et al 1997). At z > 4 the evolution appears to be accelerating, with increasing from a value just below 3 to 5.5 (Williger et al 1994).

EVOLUTION OF THE MEAN ABSORPTION     Similar numbers are obtained by methods which do not depend on line counting. For 2.5 < z < 4.5, Press et al (1993), measuring _eff(z), derived = 2.46 ± 0.37. Zuo & Lu (1993), deriving D_A from spectra reconstituted from published absorption line lists, find = 2.87 ± 0.23, but they considered a broken power law with = 2.82 below and 5.07 above z = 3.11 to give a better fit, which is in agreement with an upturn at the highest redshifts. The evolution of the mean absorption _eff or D_A is indeed a more robust measure of change, but its relation to the number of clouds is not entirely straightforward as a model has to be relied on for the distribution of absorbers, 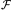(N, b, z),the functional form of which is a priori unknown. Although usually not taken into account, there clearly is mutual dependence of N, b, and z in the form of clustering, and of differential evolution in N and b. Moreover, the column density of the lines dominating the absorption changes with redshift (at z ~ 3 lines with logN(HI) ~ 14 contribute most), and so does the range of column densities to which the measurements of _eff are most sensitive.

To the surprise of many the first studies with HST of low redshift (z < 1.5) Ly lines (Morris et al 1991; Bahcall et al 1991, 1993; Impey et al 1996) (see also the paragraph on the low z Ly forest below) have discovered more absorption systems than expected from a naive extrapolation of any of the high z power law exponents. Moreover, the low = 0.48 ± 0.62 valid from z ~ 0 to z ~ 1 gives a d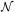 / dz that is consistent with a constant comoving density of objects. Accordingly, single power law fits attempting to explain both high and low z absorbers fail to account for the rapid upturn around z ~ 1 (e.g., Impey et al 1996).

DIFFERENTIAL EVOLUTION AS A FUNCTION OF LINE STRENGTH     A number of authors have made the case for differential evolution, as a function of column density or equivalent width. At the high column density end, Lyman limit systems (log N > 17) were found to be consistent (Lanzetta 1988; Sargent et al 1989) with a non-evolving population at least out to z = 2.5. Therefore the lower column density systems must be evolving faster, given the above values. Murdoch et al. (1986) and Giallongo (1991) noted a general tendency toward for slower evolution of with increasing W threshold, which could provide continuity between the large for the general line population and the non-evolving, optically thick Lyman limit regime. However, other studies claim the opposite trend. Bechtold (1994) found that increased from 1.32 ± 0.24 (for weaker lines (W > 0.16 Å) to 1.89 ± 0.28 for strong lines (W > 0.32 Å), Similar conclusions are reached by Acharya & Khare (1993). Bechtold's weakest lines (0.16 < W < 0.32 Å) are consistent with no evolution all, a result in agreement with the Keck study by Kim et al (1997). The latter group, and Giallongo (1991) based their conclusions on high resolution data, whereas the other papers cited are based on low resolution. Blending cannot be the whole explanation, since the present discrepancy persists regardless of resolution.

CONCLUSIONS     We may summarize the more secure results on number evolution as follows: Going from z = 0 to z ~ 1 there is no obvious change in the comoving number of the clouds. Then between 1 < z < 2 a steep rise sets in, which can be reasonably described by a power law (1 + z) with index 2 < < 3. At redshifts approaching z ~ 4, the upturn appears to steepen further. Thus a single power law does not fit the curvature of the d / dz vs. z relation well. Differential evolution, with stronger lines evolving less rapidly must exist to reconcile the large for most of the forest lines with the non-evolving population of Lyman limit absorbers. Some studies suggest that the line density at the very low column density range does not evolve much either, in which case the rapid evolution inbetween is caused either by a genuine, rapidly changing sub-population, or by biases in the analysis which we do not understand properly. In any case, the average optical depth is evolving strongly with _eff (1 + z)⁺¹ and around 2 - 3 (for 3).