1. THE THERMAL HISTORY OF MATTER

The first scientific evidence for a non-static universe came with the formulation of the theory of General Relativity by Einstein in 1915, following a completely new interpretation of the nature of the gravitational force. The basic idea is that the presence of matter alters the geometry of space-time. Test-particles follows the geodesics in space-time, which determine their orbits.

Quantitatively this idea is expressed by equating a geometry tensor G_µ (which incorporates the ten curvature terms required to specify the geometry) to a matter tensor T_µ which contains all the information (ten terms) about the mass-energy present in the manifold. (G is Newton's constant)

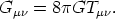
(1)

In a simplified model in which the universe is represented as an homogeneous isotropic fluid (an approximation suggested by the homogeneous distribution of galaxies in space) this equation reduces to a much simpler equation for R: the distance between any two objects (galaxies for instance) in the universe. (Here (R⁰) is the time derivative of R).

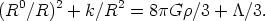
(2)

The space-time curvature terms are on the left-hand side of the equation. The first term: (R⁰/R)² is the time curvature while the second one: k/R² is the space curvature. The value of k is normalized to take one of the three values: k = 0 (flat universe), +1 (closed universe) or -1 (open universe). The gravitational effect of matter is represented by the energy density . The last term is the famous cosmological constant. Mathematically it is a sort of a priori undetermined constant of integration.

It is this equation which historically gave the first indication that our universe may not be static. It equates the time derivative of the scale factor R(R⁰) to a sum of terms which has no obvious reason to be zero.

Einstein decided to give to the exact numerical value required to obtain R⁰ = 0. This decision was most unfortunate. Einstein failed to make the important discovery that the universe is not static. Furthermore it was soon shown that his solution is not stable. Even if is (arbitrarily) chosen to neutralize the time derivative of R today, any density perturbation would suffice to bring the fluid out of this unstable equilibrium and induce a general motion one way or the other (contraction or expansion).

After 1930, thanks to the work of Edwin Hubble, the systematic motion (recession) of the galaxies was detected. The observations gave the relation R⁰/R = cst = H, where H is the Hubble constant. The value of H is still uncertain by a factor of two. It lies between 50 and 100 km/sec/megaparsec. The inverse of this parameter has the dimension of a time: the time scale of the universal expansion. Its value lies between 10 and 20 billion years.

Soon after this detection, models of the expanding universe were presented by Friedman, Lemaitre, and Alpher, Herman, Gamov. Assuming an homogeneous fluid of ideal gases, the T_µ simplifies to its diagonal form containing (, - P, - P, - P) where P is the pressure and the density of the fluid. The dynamics is given by eq. 2. The energy-momentum conservation expression, T_µ; = 0, simplifies to the following equation:

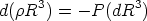
(3)

The equation T_µ; = 0 implies that the entropy per comoving volume S = sR³ remains constant which, in turn, requires that:

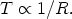
(4)

The entropy per unit volume s, given by s = ( + P)/T, decreases with R^-3, just as the number-density of particles.

One should be careful about these two last equations. They assume that entropy generating processes are operating in the fluid. In the standard mode this is guaranteed by the hypothesis of a fluid of pure non-interacting particles (except by gravitational interactions). In the real world these equations are valid only when entropy generating processes are negligibly small. This is correct most of the time. There are important chapters of cosmic expansion when this is not true, and appropriate corrections have to be made.

Eqs. (3, 4) need to be completed by an equation of state for the fluid. Three regimes are important during cosmic expansion: radiation, matter, and vacuum.

A) When the universe is radiation dominated, i.e., when the largest contribution to the energy density is due to relativistic particles (kT >> Mc²), we have T⁴ and the pressure term is one-third the density term (P = 1/3). From eqs. (3, 4) we get: R^-4 or R 1/T as expected from entropy conservation. The entropy density s is proportional to the number-density of relativistic particles, with a numerical factor of 7.1.

This regime applies to the early hot universe. Consider eqs. ((3, 4) again. Through the work of Hubble we know that R increases with time. At early moments, the density term R^-4 dominates the k/R² and the cosmological constant. Thus we have (R⁰/R) R^-2 or R t^1/2 where t is the timescale of the universe.

B) For a matter dominated (cold) universe the pressure of the non-relativistic particles is negligible compared to their mass density. P = 0.

Using eqs. (3, 4) again, we find R^-3 T³. This time we have R t^2/3.

C) In recent works, a third regime has been shown to be of great importance in the early universe. At certain times, the energy-density is dominated by the so-called vacuum energy terms associated with various physical phase transitions. These terms, which do not appear in the standard classical fluid model described before, are related to the quantum field description of matter. The undetermined cosmological constant of Einstein has become a convenient way to introduce these terms in the formalism. The equation of state of this regime is (P = -), hence = cst from eqs. (3, 4) (note the strange result that the vacuum density does not change during the expansion ...). And we have R exp(t/t₀); an exponential rate of expansion called inflation.