1.3. Cosmic Timescales

Of major importance for our subject is the temperature behaviour of the various timescales involved in the physics of the expansion. We distinguish the macroscopic timescale related to the expansion and the various microscopic timescales related to the particle reaction rates.

1.3.1. The expansion timescale

As discussed before, in the early universe the two dominant terms of equation (2) yield the simple relation (R⁰/R)² = 8G / 3 or

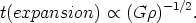
(5)

The energy density is then dominated by all the relativistic particles i (kT >> Mc²) for which _i g_iT_i⁴ where g_i is the statistical multiplicity factor (g_i = 2 for the photons). A demographical factor g^* is usually introduced to represent the effect of all the particle species on the mass-density of the early universe;

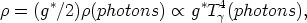
(6)

where T is the temperature of the photon gas. For reasons to be discussed shortly, the various relativistic gases may not be at the same temperature. fact will influence their density contribution and will appear in the expression for g^* in the following way

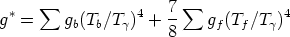
(7)

The factor 7/8 reflects the difference of the statistics for bosons, (b), and fermions, (f). At one MeV for instance, the standard demography consists of electrons and positrons, three types of neutrinos and their antineutrinos (in the standard model of elementary particles) and the photons. This gives g^* = 9.75.

Thus we get the cosmic expansion timescale as (see fig. 1)

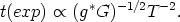
(8)

1.3.2. The reaction timescales

For the reaction timescale, let us consider a reaction of the type A + B 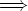C + D. For instance the capture of a neutrino by neutron to give an electron and a proton.

The capture cross-sections are function of the energy with a given power (usually positive). The probability of one capture event is given by the value of the product of the cross-section times the relative velocity: <v>, averaged over the velocity distribution pf particles at temperature T. This average value will be proportional to the strength of the interaction, G, times a certain power m of the temperature. For the weak interaction implied in the neutrino capture reactions, m = 2 and the Fermi constant G_F appears squared <v> (weak) G_F²T².

The probability of reaction per unit volume is proportional to <v> times the number-density of capturing particles per unit volume n(T) which, in the expanding universe, is n(T) T³. Thus the lifetime t(reac) for a given neutrino (in our example) to interact with neutrons (the inverse of the reaction probability) is given by (see fig. 1):

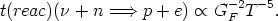
(9)

For other reactions the temperature negative exponent will be (m + 3) which, for all physical processes of importance here, will always be larger than the exponent value of 2 characteristic of the expansion timescale. The result is that the reaction timescales are always shorter than the expansion timescale in the very early universe. The two curves meet (fig 1) 1 at a certain temperature, called the decoupling temperature T_d which is a function of many parameters such as the ratio of the coupling constants (G), the demography of the universe (through g^*) and other factors influencing the cross-sections, including its energy dependance (through the power m).

Figure 1. Decoupling of the neutrino interactions. The abcissa gives the cosmic temperature and the ordinate, the age of the universe in seconds. The curve t(exp) gives the relation between cosmic age and temperature (t(exp) 1/[(GN)1/2T2]) in the standard Big-Bang. The t(reaction) curve is the mean reaction time for weak interactions involving neutrino capture and emission, (t(reaction) 1 / (GF2 T5). Cosmic time runs from right to left. At temperatures below the crossing of the curves (at the decoupling temperature T(decoupling) 1 MeV), the neutrino interactions are too slow to keep pace with the expansion and the neutron-proton equilibrium abundance is no more insured. An increase in the mass of the W particle would decrease the value of the Fermi constant (GF MW-2) and shift the reaction-time curve t'(reaction) to the right in the diagram, leading to a higher decoupling temperature T'(decoupling). On the upper part of the diagram, the n/p ratio is shown as a function of temperature. On the right part of the figure, the abundances are given by the Boltzman equilibrium equation; on the left part, the neutrons are freely decaying. On the scale at the right is given the resulting helium abundance. The position of the decoupling T can be altered by changing GF or GN as seen from the expressions for the timescales. The BBN turns out to be a very sensitive test of the rm constancy of the coupling constants.

One very important consequence of this comparative behaviour of the time scale is that all the physical processes are in statistical equilibrium at early moments of the expansion. The relative abundances of the reacting particles are then given by the law of mass-action, such as the law of Boltzman, and are independent of the past situations. After decoupling, on the contrary, the processes occur in a state of disequilibrium and the abundances reflect the past history.

For the weak interactions the decoupling temperature is given by equating eqs. (8) and (9):

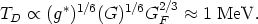
(10)