7.2. Order parameters of the phase transition

An interesting analogy can be drawn with electric conductivity (Satz 1985). A dilute gas of atoms is an insulator. The electrons, bound to their atomic nucleus, are not free to jump from one atom to another. However as the gas is compressed, the presence of the other atoms becomes increasingly important.

When the average distance between the atoms becomes comparable to the atomic radius, the orbital electrons start to feel the presence of other electrons. Their atomic electrostatic long-range potential, V(r) = 1/r, is effectively screened by the presence of these other charges. This is described in terms of the Debye screening radius (r_d = n^-1/3) where n is the number density by introducing a modified short-range potential V(r) = exp(-r / r_d) / r. The net result is the ionization of the outermost electrons and the onset of electric conductivity.

The substance undergoes a phase transition from insulation to conduction. The conductivity jumps, more or less suddenly, from zero to a finite value. Thus the conductivity can be considered as an order-parameter of the transition, in the usual sense of statistical physics.

In a similar fashion, the long-range potential between two given quarks in a low density nucleonic gas is modified by the presence of intervening quarks and gluons, when the gas is compressed to nuclear densities. As we try to separate two quarks, the potential V between them diverges rapidly at low density but remains finite at high density, i.e., when the mean interquark distance becomes smaller than one fermi.

To describe the transition, we define an order parameter L = exp(-V(r) / T) where T is the temperature. This parameter (the Wilson line or the Polyakoff loop) jumps from the zero value at low density to a finite value at high density. This jump, at T_c, is the signature of the confinement phase transition.

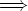
As mentioned before, another phase transition occurs during this time. In the standard QCD theory, the quarks are, by definition, massless. The lagrangian is chiral-symmetric (invariant to the transformation ( ₅ ). This implies that it does not contain a term in ( ⁺), which would not be invariant under this transformation. This is equivalent to the statement that the quark masses are zero.

In the glue, because of the very high energy density, the quarks effectively behave as massless particles. The left and right parity components of their fields do not mix. But this is not the case in our low-temperature world, where the quarks do have a mass. In the frame of the theory, the mass can only be acquired by a spontaneous breaking of chiral symmetry.

The extent of the symmetry breaking can be evaluated through the value of the term ( ⁺). The expectation value of such a term is, in fact, a measure of the effective mass (square) of the quarks in the actual physical situation. It is used as the order parameter of the chiral transition.

Because of the strength of the nuclear force, the methods of perturbation can not be used in the transition region. One needs to do QCD numerical calculations on networks, as initiated by Ken Wilson. Several groups have already presented their results with various mesh sizes and various simplifying approximations. Definite conclusions are still to come.

The low nucleonic density region (mesonic area) has been explored more extensively than the nuclear density region (nucleonic area). Progressive reduction in the mesh size gives good indications that, in this range, the two transitions are simultaneous (at T_c = T_ch 200 MeV) and first order. The situation in the nucleonic area is still highly uncertain.