Let's now analyze with some detail the behaviour of the dust corrected curve of Figure 9.
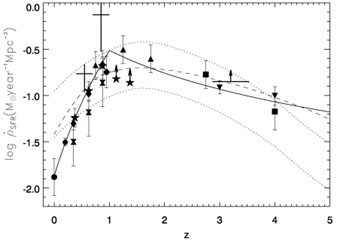
Figure 10 shows the corrected curve together with some representative theoretical models; (the details of the different sets of data are listed in table 3). Our basic assumption is that the main results from our sample of galaxies in the nearby universe are also applicable to samples of starforming galaxies at intermediate and high redshift.
|
Figure 10. The unbiased SFR density as a
function of redshift. The dotted lines represent
the two normalizations in
Somerville et al. (2001)
|
An important result is that within observational errors, our calibrations succeed in bringing into reasonable agreement the FIR determinations with the optical/UV ones. A first implication of this agreement is that large dust extinction corrections are not favoured. It can be seen that while the general trend present in previous determinations of the star formation history is preserved, the rise from z = 0 to z = 1 is steeper than in most previous work. The procedure we have used minimizes any systematic differences between the different redshift ranges and implies that, provided the composition of the sample of objects at intermediate and high redshift is similar to that of our nearby sample, the shape of the curve would be preserved.
The general behaviour of the star formation history of the universe
can be represented with a steep rise in the SFR rate
from z = 0 to z = 1 with SFR
(1 +
z)4.5
and a decline from z = 1 to z = 4 where SFR
(1 +
z)-1.5 (see solid lines
in Figure 10). The steep increase to z =
1 is similar to the slope found by
Glazebrook et al. (1999)
using the H
luminosities
only.
We are confident that the procedure presented in this paper guarantees the removal of systematic differences between the star formation estimators when they are applied to samples qualitatively similar to ours. This in turn means that the general shape and in particular the slope from z = 0 to z = 1 and from z = 1 to z = 4 are well determined, although the exact value of the z = 0 to z = 1 slope is still very dependent on the exact value of the SFR in the nearby universe.
We also included in Figure 10 the results from
some representative
semi-analytical models of galaxy formation corresponding to the
hierarchical cold dark matter scenario. The dotted lines correspond to
Somerville et al. (2001)
CDM models with two
different normalizations
while the dashed line corresponds to model C from
Baugh et al. (1998).
Whatever the local value of the SFR is, the comparison with these models of galaxy formation shows a general agreement in the shape plus what we can call a local excess in the models, i.e. the models have a shallower slope between z = 0 to z = 1 than the data suggest or equivalently, that present semi-analytical models of galaxy formation seem unable to reproduce the sharp increase in the SFR from z = 0 to z = 1.