3. INFLATION + CDM IN THE ERA OF PRECISION COSMOLOGY

As we look forward to the abundance (avalanche!) of high-quality observations that will test Inflation + CDM, we have to make sure the predictions of the theory match the precision of the data. In so doing, CDM + Inflation becomes a ten (or more) parameter theory. For astrophysicists, and especially cosmologists, this is daunting, as it may seem that a ten-parameter theory can be made to fit any set of observations. This is not the case when one has the quality and quantity of data that will be coming. The standard model of particle physics offers an excellent example: it is a nineteen-parameter theory and because of the high-quality of data from experiments at Fermilab's Tevatron, SLAC's SLC, CERN's LEP and other facilities it has been rigorously tested and the parameters measured to a precision of better than 1% in some cases. My worry as an inflationist is not that many different sets of parameters will fit the upcoming data, but rather that no set of parameters will!

In fact, the ten parameters of CDM + Inflation are an opportunity rather than a curse: Because the parameters depend upon the underlying inflationary model and fundamental aspects of the Universe, we have the very real possibility of learning much about the Universe and inflation. The ten parameters can be organized into two groups: cosmological and dark-matter (Dodelson et al, 1996).

1. h, the Hubble constant in units of 100 km s^-1 Mpc^-1.

2. _B h², the baryon density. Primeval deuterium measurements and together with the theory of BBN imply: _B h² = 0.02 ± 0.002.

3. n, the power-law index of the scalar density perturbations. CBR measurements indicate n = 1.1 ± 0.2; n = 1 corresponds to scale-invariant density perturbations. Several popular inflationary models predict n 0.95; range of predictions runs from 0.7 to 1.2 (Lyth & Riotto, 1996).

4. dn / dln k, "running" of the scalar index with comoving scale (k = wavenumber). Inflationary models predict a value of ( ± 10^-3) or smaller (Kosowsky & Turner, 1995).

5. S, the overall amplitude squared of density perturbations, quantified by their contribution to the variance of the CBR quadrupole anisotropy.

6. T, the overall amplitude squared of gravity waves, quantified by their contribution to the variance of the CBR quadrupole anisotropy. Note, the COBE normalization determines T + S (see below).

7. n_T, the power-law index of the gravity wave spectrum. Scale-invariance corresponds to n_T = 0; for inflation, n_T is given by - 1/7 T/S.

1. , the fraction of critical density in neutrinos (= _i m_i / 90h²). While the hot dark matter theory of structure formation is not viable, it is possible that a small fraction of the matter density exists in the form of neutrinos. Further, small - but nonzero - neutrino masses are a generic prediction of theories that unify the strong, weak and electromagnetic interactions - and the Super-Kamiokande Collaboration has presented evidence that the at least one of the neutrino species has a mass of greater than about 0.1eV, based upon the deficit of atmospheric muon neutrinos (Fukuda et al, 1998).

2. _X, the fraction of critical density in a smooth component of unknown composition and negative pressure (w_X - 0.3). There is mounting evidence for such a component, with the simplest example being a cosmological constant (w_X = - 1).

3. g_*, the quantity that counts the number of ultra-relativistic degrees of freedom (around the time of matter-radiation equality). The standard cosmology/standard model of particle physics predicts g_* = 3.3626 (photons in the CBR + 3 massless neutrino species with temperature (4/11)^1/3 times that of the photons). The amount of radiation controls when the Universe became matter dominated and thus affects the present spectrum of density inhomogeneity.

3.1. Present status of Inflation + CDM

A useful way to organize the different CDM models is by their dark-matter content; within each CDM family, the cosmological parameters vary. One list of models is:

1. sCDM (for simple): Only CDM and baryons; no additional radiation (g_* = 3.36). The original standard CDM is a member of this family (h = 0.50, n = 1.00, _B = 0.05), but is now ruled out (see Fig. 3).

2. CDM: This model has extra radiation, e.g., produced by the decay of an unstable massive tau neutrino (hence the name); here we take g_* = 7.45.

3. CDM (for neutrinos): This model has a dash of hot dark matter; here we take = 0.2 (about 5eV worth of neutrinos).

4. CDM (for cosmological constant): This model has a smooth component in the form of a cosmological constant; here we take = 0.6.

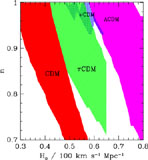
Figure 3. Summary of viable CDM models, based upon CBR anisotropy and determinations of the present power spectrum of inhomogeneity (Dodelson et al, 1996).

Figure 3 summarizes the viability of these different CDM models, based upon CBR measurements and current determinations of the present power spectrum of inhomogeneity derived from redshift surveys. sCDM is only viable for low values of the Hubble constant (less than 55 km s^-1 Mpc^-1) and/or significant tilt (deviation from scale invariance); the region of viability for CDM is similar to sCDM, but shifted to larger values of the Hubble constant (as large as 65 km s^-1 Mpc^-1). CDM has an island of viability around H₀ ~ 60 km s^-1 Mpc^-1 and n ~ 0.95. CDM can tolerate the largest values of the Hubble constant.

Considering other relevant data too - e.g., age of the Universe, determinations of _M, measurements of the Hubble constant, and limits to - CDM emerges as the "best-fit CDM model" (Krauss & Turner, 1995; Ostriker & Steinhardt, 1995; Liddle et al, 1996); see Fig. 4. Moreover, its "smoking gun signature," negative q₀, has apparently been confirmed (Riess et al, 1998; Perlmutter et al, 1998). Despite my general enthusiasm, I would caution that it is premature to conclude that CDM is anything but the model to take aim at.

Figure 4. Constraints used to determine the best-fit CDM model: PS = large-scale structure + CBR anisotropy; AGE = age of the Universe; CBF = cluster-baryon fraction; and H0= Hubble constant measurements. The best-fit model, indicated by the darkest region, has h 0.60 - 0.65 and 0.55 - 0.65.