Copyright © 1997 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1997. 35:
445-502 Copyright © 1997 by Annual Reviews. All rights reserved |
4.2. Inversion Methods, Cross-Correlations, and Modeling
Methods of echo mapping are presented in numerous papers (e.g.
Blandford & McKee
1982;
;
Krolik et al 1991)
and in conference proceedings
(Gondhalekar et al
1994).
The light curve of a given line, L(t), can be considered as a
convolution of the continuum light curve, C(t), and a transfer
function (TF), 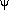 (
( ):
):
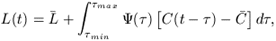 (2)
(2)
where 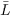 and
and
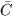 are the mean of the line and continuum intensities, respectively.
The transfer function (the kernel) is a map showing where
the line emission is produced in each
interval of time delay by the gas along the
paraboloid surfaces of constant delay. This can be
generalized to give the time delay distribution
at each velocity in the line profile.
are the mean of the line and continuum intensities, respectively.
The transfer function (the kernel) is a map showing where
the line emission is produced in each
interval of time delay by the gas along the
paraboloid surfaces of constant delay. This can be
generalized to give the time delay distribution
at each velocity in the line profile.
A powerful and flexible inversion method is the Maximum Entropy Method, MEM (Horne 1994), especially in its velocity-resolved form, but less computationally expensive linear methods have also been proposed (Pijpers 1994, Krolik & Done 1995). The results of numerical techniques for inverting Equation 2 have been limited by the intrinsic indeterminacy of any inversion problem in the presence of noisy data collected at uneven time intervals (e.g. Vio et al 1994). Several authors have calculated theoretical velocity-delay maps for plausible BLR configurations and velocity fields (Perez et al 1992a, b, Goad et al 1993) for comparison with the result of the inversion of Equation 2.
A simpler estimate of the linear scale of the BLR comes from cross-correlating the line and continuum light curves. The peak of the cross-correlation function represents the material closest to the ionizing source, while the centroid gives an emissivity-weighted average time delay over the emission region (Edelson & Krolik 1988, Perez et al 1992a, b). These estimates are not unique, as they try to encapsulate in a single number the time-delay distribution of the emitting clouds. Note that the centroid of the transfer function can be obtained directly from the line-continuum cross-correlation function (Koratkar & Gaskell 1991, Robinson 1995).