4.5. Another global test : the baryon fraction in local clusters

This is a very interesting test proposed by White et al. (1993) which in principle offer a rather direct way to measure _m. It relies on one side on the fact that one should be able to measure the total mass of clusters, as well as their baryon content and on the other side that the primordial abundance of baryons can be well constrained from the predictions of primordial nucleosynthesis and the observed abundances of light elements. Furthermore, the CMB is providing interesting constraints on the baryon density of the universe, that are essentially consistent with values inferred from nucleosynthesis (Eq. 1). X-ray observations of clusters allow to measure their gas mass which represents the dominant component of their (visible) baryonic content (the stellar component represents around 1% of the total mass). In this way one can measure the baryon fraction f_b and infer _m:

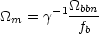(6)

where represents a correction factor between the actual baryon fraction and the naive value _bbn / _m; typically, ~ 0.9. This method has been used quite often (Evrard, 1997; Roussel et al., 2000). There are some differences between measurements, mainly due to the mass estimators used. One key point is that the baryon fraction has to be estimated in the outer part of clusters as close as possible to the virial radius. However, the outer profile of the X-ray gas has been shown by Vikhlinin et al. (1999) not to follow the classical profile, usually assumed, but being actually steeper; consequently derived gas masses are somewhat lower than from usual analysis. Recently, several consequences of this work were derived on the baryon fraction (Sadat and Blanchard, 2001):

• the scaled baryon fraction flattens in the outer part of clusters.
• the global shape of the baryon fraction from the inner part to the outer part follows rather closely the shape found in numerical simulations from the Santa Barbara cluster project (Frenk et al, 1999).
• when mass estimates are taken from numerical simulations the baryon fraction, corrected from the -rather uncertain- clumping factor (Mathiesen et al, 1999) could be as low as 10% (h = 0.5).

The consequence of this is that a value of _m as high as 0.8 can be acceptable. Large systematic uncertainties are still possible, and value twice lower can certainly not be rejected on the basis of this argument, but similarly a value _m ~ 1 can not be securely rejected.