


2.1.1. Basic formalism
For all coordinate types, the first step is a linear transformation applied via matrix multiplication of the vector of pixel coordinate elements, pj:
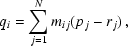 |
(1) |
where rj are the pixel coordinate elements of the reference point given by the CRPIXj. Henceforth we will consistently use j for pixel axis indexing and i for the world axes.
The mij matrix is a non-singular square matrix of dimension N × N. In the first instance, N is given by the NAXIS keyword value, but this will be generalized with the introduction of the WCSAXES keyword in Sect. 2.2 so that the dimension of the world coordinates need not match that of the data array.
The elements, qi, of the resulting intermediate pixel coordinate vector are offsets, in dimensionless pixel units, from the reference point along axes coincident with those of the intermediate world coordinates. Thus the conversion of qi to the corresponding intermediate world coordinate element, xi, is a simple scale:
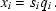 |
(2) |
We defer discussion of the encoding of mij and si as FITS header cards to Sect. 2.1.2.
The third step in the process of computing world coordinates depends on the CTYPEi. For simple linear axes, the xi are interpreted as offsets to be added to the coordinate value at the reference point given by CRVALi. Otherwise, the CTYPEi define a function of the xi, the CRVALi, and, perhaps, other parameters that must be established by convention and agreement. Any CTYPEi not covered by convention and agreement shall be taken to be linear.
Non-linear coordinate systems will be signaled by CTYPEi in "4-3" form: the first four characters specify the coordinate type, the fifth character is a "-", and the remaining three characters specify an algorithm code for computing the world coordinate value, for example 'ABCD-XYZ'. We explicitly allow the possibility that the coordinate type may augment the algorithm code, for example 'FREQ-F2W' and 'VRAD-F2W' may denote somewhat different algorithms (see Paper III). Coordinate types with names of less than four characters are padded on the right with "-", and algorithm codes with less than three characters are padded on the right with blanks, for example 'RA-UV '. However, we encourage the use of three-letter algorithm codes.
Particular coordinate types and algorithm codes must be established by convention. Paper II constructs the framework for celestial coordinate systems, and Paper III does so for spectral axes (frequency-wavelength-velocity). CTYPEi values that are not in "4-3" form should be interpreted as linear axes. It is possible that there may be old FITS files with a linear axis for which CTYPE i is, by chance, in 4-3 form. However, it is very unlikely that it will match a recognized algorithm code (use of three-letter codes will reduce the chances). In such a case the axis should be treated as linear.