2.1.3. Usage comments

The proposal presented in this and the subsequent papers is not simple and provides wide latitude for mistakes in describing the WCS and in writing the FITS headers. The result of an improperly described WCS is simply undefined; it is the job of the FITS writer to produce a correct description. A simple error which could be made in a WCS description, or with other parts of a header, is a repetition of keywords with different values assigned to them. If, for example, BUNIT were repeated with a new value, the data would have unknown units but would be read correctly. In binary tables, a second value for TFORMn would cause the tabular data to be read incorrectly.

This is a very general proposal! The linear transformation matrix allows for skew and fully general rotations. The reader should note that this allows dissimilar axes to be rotated into one another. This is meaningful in imaging; for example, one may wish to re-sample a spectral-line cube from some special viewing angle in the three-space of two celestial coordinates and one frequency coordinate. Such rotations are, however, forbidden into axes whose coordinate values are, by convention, only integral. Thus, if CTYPEi₀ indicates a world coordinate of integral type, then row i₀ of the linear transformation matrix must contain only one non-zero element, and this would normally be 1.0 or at least integral. Additionally, it must be the only non-zero element in the column containing it. The STOKES axis is one such coordinate; see Sect. 5.4.

The linear transformation matrix could also be used to represent images that have been transposed, e.g.

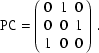This is a legal usage, but likely to confuse the reader. In this example, the FITS user will read in the header that the first element of the world coordinate is CTYPE1, although this corresponds to the second pixel axis. Note that keywords NAXIS1, CRPIX1, PCi_, and CDi_, for example, all refer to the first pixel axis in the image, while CTYPE1, CRVAL1, PC_j, CD_j, and CDELT1 all refer to the first world coordinate ("q₁" and "x₁") element. They must produce a correct result when Eqs. (1) and (2) or Eq.(3) are applied. Thus, x₁ is of type CTYPE1 even if it does not change with p₁ (to use the nomenclature of Eqs. (1), (2), and (3)). Therefore, it is good form to transpose the header parameters along with the image so that the on-diagonal terms in the transformation matrix predominate. If the PC or CD matrix is essentially diagonal, then the human reader of the FITS header will have a better chance of understanding the coordinate representation.

Equations (1) and (2) allow considerable flexibility in the way the linear transformation is partitioned between the PCi_j and CDELTi. In the absence of any formal constraints, the normal expectation would be that the CDELTi be used as scaling parameters as in the past. This is straightforward if PCi_j is orthogonal, i.e. defines a pure rotation or simple reflection, but not if it has an element of skewness. In general, a reasonable approach is to choose CDELTi so that

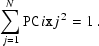(4)

for all i. This normalization leaves orthogonal matrices unchanged, and only slightly modifies matrices which are nearly orthogonal. Note that this is not the same as setting the determinant of the PCi_j matrix to unity. Note also that this constraint is optional and may not be the most physically meaningful selection of the PCi_j. For example, the conversion from the old CROTAi nomenclature to the new PCi_j form described in Paper II does not satisfy this constraint unless the CDELTi are equal.