


2.1. Problems of Recognition of Double Galaxies
Looking at photographs of some small region of the sky, it is easy to convince oneself that the number of galaxies with small separations and nearly matching apparent magnitudes or angular diameters notably exceeds the expected number for a uniform random distribution. The reason for this observation lies in the existence of double and multiple systems. If radial velocities were known for all galaxies, the recognition of physical pairs would not constitute any special problem. However, in a typical situation, the radial velocities of the galaxies are not known. Only recently, Huchra et al. (1983) presented a large survey of radial velocities for galaxies brighter than magnitude 14.5 covering high galactic latitudes. Therefore, a realistic expression for recognition of double galaxies must be formulated operating on apparent angular separation, Xij, apparent magnitude mi, and angular diameter of the galaxies ai. As is well known, the distribution of galaxies in linear diameter and luminosity has a very large dispersion. Because of this, the observed quantities ai and mi are very poor indicators of the distribution of the distance of galaxies from the observer, which reduces the effectiveness of the desired criterion for pairs of galaxies. Sometimes, for physical reasons, two galaxies exhibit signs of interaction between them. However, the description of such signs of interaction is normally qualitative and subjective in character, which makes such notation unsuitable for any strict criterion for double systems.
In section 1.2, we remarked on some weak points of the pair criterion proposed by Holmberg. We will note here two such unsatisfactory aspects. For a uniform distribution of galaxies in depth it is always possible to find around some fixed galaxy of angular diameter a1, another faint enough galaxy of diameter a2 which is projected on the plane of the sky at an angular separation x12 from the first. Therefore the criterion of Holmberg
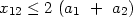 |
(2.1) |
is formally satisfied by every galaxy in the sky. To resolve this paradox it is apparently necessary to limit the galaxies considered by either apparent magnitude or angular diameter. Most probably, two galaxies with very different angular diameters result from the chance projection of very distant and rather nearby galaxies. Therefore, a criterion for pairs of galaxies should incorporate photometric limits in the selection of these galaxies. Such a selection should be applicable uniformly across the sky for purposes of standardization.
Another shortcoming of criterion (2.1) is its conservativeness. The Holmberg expression (2.1) excludes wider pairs in which the separation between components is noticeably greater than the size of the galaxies. In fact, the Holmberg criterion includes only very tight, contact systems.
Further discussions of various approaches to recognising double galaxies are given in the monographs by Agekyan (1970) and Vorontsov-Vel'yaminov (1972).
From general considerations a physical pair of two galaxies should consist of galaxies sufficiently close to each other that the energy of interaction between them and any neighbouring galaxies should be smaller than the potential energy of the interaction between the two galaxies in the pair. An expression for such dynamical isolation in a pair with respect to their nearest neighbours may be written in the form
 |
(2.2) |
where M1 and M2 are the masses of
the components of the pair, r12 is the actual
separation between the components of the pair,
Mi is the mass of the neighbouring galaxy located at
distances r1i and r2i from the members of the pair, and  is a small dimensionless quantity.
is a small dimensionless quantity.
It is not possible to apply (2.2) to the apparent distribution of the galaxies, since the masses of galaxies and their actual separations are, in general, unknown. Therefore, for practical use, expression (2.2) must be replaced by one incorporating the observed quantities; that is, the apparent separation between galaxies, their apparent magnitudes, and/or their angular diameters. Such a transformation may be attempted in various ways. By a qualitative analog to (2.2), Karachentsev (1970a) proposed
 |
(2.3) |
where mk is the apparent magnitude of the galaxy and
xki is the angular separation between galaxies.
The other indices have the same form and meaning as in (2.2).
The transformation from (2.2) to (2.3) presupposes that the masses
of galaxies are proportional to their luminosity.
If in defining pairs we look only at bright neighbouring galaxies
with apparent magnitude mi < m1
 m2, then
according to (2.3)
x1i
m2, then
according to (2.3)
x1i  x2i
and the expression for isolation may be presented very simply
x2i
and the expression for isolation may be presented very simply
 |
(2.4) |
Experience shows that the required correlation (2.4) for the masses of the galaxies involved is not tight enough to be useful, so on practical grounds we made a selection using a form of isolation criterion applied to the apparent angular separation and angular diameter of galaxies.
It is appropriate to make several remarks at this point on the general problem of pair criteria. Any statistical criterion for the isolation of a pair of galaxies has two kinds of limitations. The first limitation may be expressed as the probability of including an optical pair of galaxies in the sample, that is, a pair resulting from chance superposition along the line of sight of galaxies located far from one another. The second limitation comes from the probability that a physical pair of galaxies will fail the isolation criterion and not appear in the catalogue. To produce a criterion of the highest effectiveness, both kinds of limitations should be recognised and their effects minimized.
The study of the effectiveness of an isolation criterion is fraught with many difficulties. To estimate the effectiveness of such a selection, it is necessary to know the properties of the distribution of galaxies as a function of mass and of scale, the luminosity function of galaxies, and, most important, the characteristics of the distribution of double galaxies in projected separation, linear diameter, absolute magnitude and so on and so forth. Because of all these problems it is necessary to limit oneself to an empirical approach to a criterion formulated from measurable quantities.
An optimal criterion for the isolation of a pair should probably exhibit the following properties.
Various empirically formulated criteria for the isolation of galaxies were applied to the distribution of galaxies in the Palomar Survey. The effectiveness of the criterion was estimated from the cases of especially close pairs and of double galaxies with apparent signs of interaction. After many trials, we adopted the following formulae for isolation of a pair of galaxies.
For possible members of a double system we examined galaxies from the Zwicky Catalogue (CGCG) with apparent magnitudes
 |
(2.5) |
which ensures the photometric uniformity of the selection. Two such galaxies with angular diameter a1 and a2 and mutual angular separation x12 were considered to satisfy the isolation criteria with respect to galaxies seen nearby in projection if
 |
(2.6) |
where the index i indicates each neighbouring galaxy whose angular diameter ai occurs in the intervals
 |
(2.7) |
The last expression applied pair-wise to the search for double systems indicates that in (2.6) we need to consider only `significant' neighbours, which are galaxies not very different in size from the pair members. It is important to note that significant neighbours may be galaxies fainter than the limit of magnitude 15.7. Therefore, ensuring the isolation of a pair often requires examining the Palomar charts for the large numbers of galaxies not appearing in the CGCG.
For the basic criterion in the catalogue, we adopted the following values for the dimensionless coefficients
 |
(2.8) |
Therefore, if all galaxies have the same angular diameter (identical particles), then according to (2.6) through (2.8) a neighbour of a pair of galaxies should be located on the sky more than five times farther from a pair than the separation of the pair members from each other. Larger neighbouring galaxies produce a larger `zone of avoidance' around members of a pair, proportional to their angular diameters ai, in order to reduce the gravitational influence of massive neighbours on a pair. In the same way the expression for dynamical isolation of a pair is not significantly affected by a close dwarf galaxy.
In addition to this basic isolation criterion, denoted by (- -), our catalogue also includes three additional, stronger criteria, with the following parameters:
 |
(2.9) |
These are necessary in order to produce subsamples of double galaxies with smaller numbers of chance optical systems.
Schematic illustrations of isolated pairs satisfying (2.8) and (2.9) are shown in figure 1.
 |
Figure 1. Illustrations of isolated pairs of galaxies satisfying various criteria for isolation with regard to galaxies seen nearby in projection. |
The dependence of the criteria on the parameter
 can be estimated for the
case of identical particles distributed uniformly on the plane of the sky.
If around a given particle its two nearest neighbours are located
at distances x1 and x2, then the
expression x2 / x1
can be estimated for the
case of identical particles distributed uniformly on the plane of the sky.
If around a given particle its two nearest neighbours are located
at distances x1 and x2, then the
expression x2 / x1

 may be transformed into the probability
may be transformed into the probability
 |
(2.10) |
This expression is easily derived starting from the case in which the
first companion particle is uniformly distributed within
a circle of radius x2.
Therefore, the two-point poisson distribution of individual particles
will produce chance `pairs' with a probability p = 0.04 for
 = 5 and p = 0.01 for
= 5 and p = 0.01 for
 = 10.
The probability of seeing pairs among galaxies of varying diameters
is much more difficult to calculate, and a further complication is
introduced by the unrealistic assumption of a uniform distribution of
these objects on the sky.
= 10.
The probability of seeing pairs among galaxies of varying diameters
is much more difficult to calculate, and a further complication is
introduced by the unrealistic assumption of a uniform distribution of
these objects on the sky.
Expressions (2.5) to (2.8) are sufficient to calculate the data needed for isolated pairs of galaxies. The effectiveness of this criterion has been investigated by means of computer simulations of the apparent distribution of galaxies, as discussed in the next chapter.
We note that the good criteria for double systems proposed by Turner (1976a) and Peterson (1979) may be viewed as modified cases of our criterion.