3.1. Modelling the Observed Distribution of Pairs
Either for fundamental reasons or from the properties of their evolution, double galaxies may depart markedly in several respects from single galaxies, or even from members of groups or clusters. Such differences may be apparent, resulting from erroneous interpretations or failure to consider selection effects on the observations. The role of such effects is neglected rather often.
Strong selection effects accompany the isolation of pairs of galaxies from their observed properties: apparent diameters, apparent magnitudes, and projected separation. As a result the `catalogue' distribution of double galaxies may depart in several parameters from the true distribution in some volume of space. A quantitative analysis of various factors in the selection may be carried out with the methods of mathematical statistics. One such attempt was made by Neyman and Scott (1962, 1963). Unfortunately, for an analytical approach it is necessary to adopt assumptions which are unsatisfactorily far from reality. For example, a selection analysis usually begins with the assumption of a Poisson distribution of objects, which departs markedly from the actual distribution of galaxies.
In this chapter we examine the effects of selection according to various characteristics on the distribution of double galaxies, incorporating the results of computer modelling of the apparent distribution of galaxies (Karachentsev and Shcherbanovsky, 1978). For this modelling we used Monte Carlo techniques on the distribution in space and the multiplicity of galaxies in systems. As a basis the following propositions were adopted:
1) Every galaxy in a unit volume has a probability pk of membership in a system of multiplicity k, where the multiplicity of the system takes the values 1, 2, 3, 30 and 1000.
2) The centers of systems of galaxies are distributed with a constant space density. Their numbers are so chosen as to match the mean surface density of galaxies per square degree, given observationally by the CGCG catalogue.
3) The structures of different systems of multiplicity k are taken as identical. The distance of galaxies from the center of the system in each coordinate and in radial velocity are given by
 |
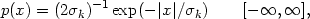(3.1) |
where the parameters
k describing
the linear scale and velocity dispersions are tabulated in
Table 3.
Because the generation of the coordinates and velocity for each galaxy
are conducted independently, the centroid of each system does
not agree with its adopted center.
The individual velocities of the galaxies are given by the sum of the
Hubble velocity of the center of the system and the peculiar component with
respect to the center, given by (3.1).
4) We adopted a step function for the luminosity function of galaxies, identical for all systems:
 |
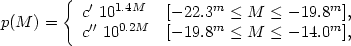(3.2) |
where c' and c" are normalisation and continuity constants. The effect of luminosity segregation with radius within the systems was ignored.
5) The apparent magnitude of the galaxy was calculated from its distance D and its absolute magnitude, m = M - 5 + 5 log D, without modelling the absorption of light in interstellar space and with no cosmological effects.
6) The angular diameter of a galaxy a (in arcminutes) is related to its apparent magnitude by
 |
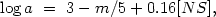(3.3) |
where [NS] is a normally distributed random variable with zero mean and unit standard deviation.
Incorporating the postulated form of the luminosity function and data from the CGCG catalogue for its limiting magnitude of 15.7, the volume modelled for structure occupies [410 by 54 by 54] Mpc3. To generate pseudo-random numbers, we incorporated a standard program with a period of 3 × 1010 numbers. Charts of the volume distribution of galaxies projected on the celestial sphere in areas of 6 by 6 degrees were generated for comparison with measurements on charts of the Palomar Atlas.
Because of limitations in our computer, modelling
every field independently was not possible.
Therefore, the galaxy luminosity function (3.2) was chosen to be high,
since otherwise
only a small fraction of the objects in the volume element would appear
above the selection limit of magnitude 15.7.
The mean number of galaxies on a 6° × 6° map is
N
75,
just as in the CGCG catalogue at high galactic latitudes.
In all, 127 fields were modelled with a total of 9433 galaxies
brighter than magnitude 15.7.
For every galaxy, in both graphical and numerical form, the computer program
presented coordinates, apparent magnitude, angular diameter, radial
velocity, distance from the observer, and membership of the galaxy in
any system of the defined types.
Examples of this realisation of the apparent distribution of galaxies are
presented in the article by
Karachentsev and
Shcherbanovsky (1978).
Comparison with fields from the Zwicky Catalogue displays
reasonably satisfactory quantitative agreement.
A more detailed confrontation between the model and real distributions
of galaxies was discussed by
Mukanov and Shcherbanovsky
(1979)
using the two-point correlation function.
The principal respect in which these Monte Carlo imitations of the distribution of galaxies are unsatisfactory lies in the rather arbitrary distributions of those parameters which are not derived directly from observed distributions on the sky. Ignoring this limitation, such modelling with its grid of variations for various parameters provides a useful approximation to use to examine these questions.
But, the more complex and refined an algorithm we adopt for realising the distribution of galaxies, the more difficult it is to analyse the results so obtained. Therefore we have kept our models simple by incorporating a non-hierarchical distribution and a small number of types of systems, as an accessible compromise. This model does satisfy the properties of the multi-scaled clustering in the apparent distribution of galaxies.
On 127 fields of this artificial CGCG catalogue, we conducted a search for double systems according to the isolation criteria (2.6) through (2.8). Just as was done for the pairs in the real catalogue, the data on the galaxy radial velocities as well as on their occurrence in systems of various multiplicities were not incorporated, to avoid including an element of subjectivity.
Overall, in the modelled fields, the basic isolation criterion was satisfied by 301 pairs of galaxies. We have used the characteristics of these pairs to analyse the basic properties of selection effects and to estimate the number of false pairs (Karachentsev, 1981c).