


3.3. The Distribution of Relative Velocities
Amongst the various properties of double galaxies, the distribution of the difference in their radial velocity, y = | V1 - V2|, is only weakly subject to selection effects. It is also clear that, since the selection of double galaxies has taken place without regard to their radial velocities, the resulting distribution p(y) includes only the effects of velocity measurement errors and the inclusion of false pairs in the sample.
The distribution of double galaxies in intervals of relative radial velocity is presented in Table 5. The second column shows the number of real pairs from the catalogue and the fourth, the number of model pairs. The three final columns show how many physical pairs (p), members of systems (s), and optical pairs (o) occur at each interval of radial velocity, for the model pairs only. In all, the distributions of K- and M-pairs show the following. About half of the double galaxies have relative velocities in the neighbourhood of 100 km/s, while the remaining parts of both samples show distributions extending upwards as far as 10000 km/s. In the final column of Table 5, it is apparent that physical pairs are strongly concentrated within y < 200 km/s, with a mean of 92 km/s. Members of systems show velocity differences ranging upwards in the region 200 - 800 km/s, with a mean for them of 207 km/s, and for y > 800 km/s, a major part of the sample is optical pairs with a mean relative velocity of 4000 km/s.
In the literature one may encounter various attempts to distinguish true
and false pairs according to the quantity y. Thus,
Turner (1976b)
proposed that physical pairs are
all those with y < 425 km/s.
In the last column of Table 5, we see that
optical pairs with such
relative velocities do indeed occur among the model systems.
Furthermore, Turner's condition does not exclude pseudo-pairs made from
members of groups and clusters.
Besides that, the limit y < 425 km/s excludes
several physical pairs consisting of very large galaxies
(for example, number 588 with y = 833 km/s), but it
appears redundant for dwarf doubles such as number 384.
We propose that to distinguish between physical and false pairs it is
necessary to take into account not only the velocity difference but also the
projected separation and brightness of the components.
We will adopt, quantitatively, that pairs of galaxies are physical systems
if their mass-to-light ratio f < 100
f , where the
calculated orbital mass-to-light ratio is given by (2.17) and (2.18).
This proposal will be incorporated in the following chapter.
, where the
calculated orbital mass-to-light ratio is given by (2.17) and (2.18).
This proposal will be incorporated in the following chapter.
The distribution of the 487 pairs with f < 100 in intervals of relative radial velocity is presented in the third column of Table 5. The mean value of the relative radial velocity for objects in this sample (137 km/s) is a factor of four smaller than that for the entire catalogue.
In order to obtain the true distribution p(y) it is
necessary to consider the errors in the measurement of velocities.
If these errors are uncorrelated for members of the pair, then the error
in the difference is

 V =
(
V =
( V12 +
V12 +
 V22)1/2 and for
the 487 pairs,
<
V22)1/2 and for
the 487 pairs,
<
 V2>1/2 = 69 km/s.
We shall suppose further, taking it as a proposition, that the value of
the radial velocity difference and the error in its measurement are not
correlated with one another. Then by inspection of selected moments
<yk> and
<
V2>1/2 = 69 km/s.
We shall suppose further, taking it as a proposition, that the value of
the radial velocity difference and the error in its measurement are not
correlated with one another. Then by inspection of selected moments
<yk> and
<
 V k>
it is easy to obtain the k-th moment of the distribution of
radial velocities, and from this to derive the distribution of relative
velocities p(y).
Forming this for the first four moments yields the exponential expression
V k>
it is easy to obtain the k-th moment of the distribution of
radial velocities, and from this to derive the distribution of relative
velocities p(y).
Forming this for the first four moments yields the exponential expression
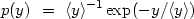 |
(3.4) |
with mean value <y> = 120 km/s.
Figure 5 shows the distribution of the 487
double galaxies according to the
observed difference in radial velocities on a logarithmic scale.
The distribution of radial velocity differences expected from (3.4)
is shown as the plotted line.
As will be shown later, the role of measurement errors
appears as a deficiency of objects in the interval
y  <
<
 V>,
thus shifting the apparent maximum in the distribution away from zero.
V>,
thus shifting the apparent maximum in the distribution away from zero.
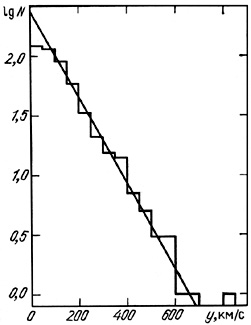 |
Figure 5. |