4.7. A worked example

It will be useful to see how all this works in the context of a specific potential. We will choose one of the simplest possible models, a massless field with a quartic self-coupling,

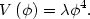(115)

This potential, simple as it is, has all the characteristics needed to support a successful inflationary expansion. We will assume up front that the field is slowly rolling, so that Eqs. (86, 87) describe the equations of motion for the field,

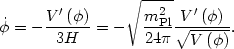(116)

In order for inflation to occur, we must have negative pressure, p < - (1/3), which is equivalent to the slow roll parameter being less than unity,

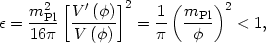(117)

so that inflation occurs when > _e = (m_Pl / ). Note that the field is displaced a long way from the minimum of the potential at = 0! This has been the source of some criticism of this type of model as a valid potential in an effective field theory [35], but here we will accept this fact at the very least as valid phenomenology.

In this simple model, then, we have inflation happening when the field is rolling down the potential in a region far displaced from the minimum > m_Pl. Inflation ends naturally at late time, when passes through _e = m_Pl / . In order to solve the horizon and flatness problems, we must have at least a factor of e⁵⁵ expansion. The number of e-folds is given by Eq. (101),

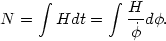(118)

It is convenient to choose the limits on the integral such that N = 0 at the end of inflation, so that N counts the number of e-folds until inflation ends and increases as we go backward in time. Then, using the equation of motion for the field, we can show that N is just an integral over the slow-roll parameter , and can be expressed as a function of the field value :

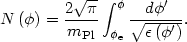(119)

For our ⁴ potential, the number of e-folds is

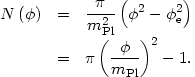(120)

Equivalently, we can define the field _N as the field value N e-folds before the end of inflation,

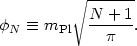(121)

We can now test our original assumption that the field is slowly rolling. It is simple to show by differentiating Eq. (116) that the acceleration of the field is given by

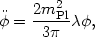(122)

which is indeed small relative to the derivative of the potential for >> m_Pl:

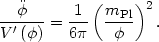(123)

We see that slow roll is beginning to break down at the end of inflation, but is an excellent approximation for large N.

The rest is cookbook. We want to evaluate the power spectrum amplitude P_S, tensor/scalar ratio r, and scalar spectral index n for fluctuations with scales comparable to the horizon size today, which means fluctuations which crossed outside the horizon during inflation at about N 55. Therefore, to calculate the amplitude P_S, we evaluate

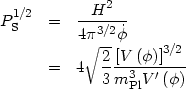(124)

at = ₅₅, or:

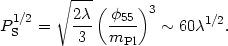(125)

But from the CMB, we know that the power spectrum amplitude is P_S^1/2 ~ 10^-5, so that means we must have a very tiny self-coupling for the field, ~ 10^-14. In order to sufficiently suppress the density fluctuation amplitude, the model must be extremely fine-tuned. This is a typical property of scalar field models of inflation. This also allows us to estimate the energy scale of inflation,

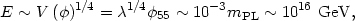(126)

or right about the scale of Grand Unification. This interesting coincidence is typical of most models of inflation.

Finally, it is straightforward to calculate the tensor/scalar ratio and spectral index,

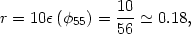(127)

and

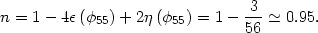(128)

The procedure for other potentials is similar: first, find the field value where inflation ends. Then calculate the field value 55 e-folds before the end of inflation and evaluate the expressions for the observables at that field value. In this way we can match any given model of inflation to its observational predictions. In the next section, we examine the predictions of different types of models in light of current and future observational constraints, and find that it will be possible with realistic measurements to distinguish between different models of inflation.