2.3. Selection effects

One characteristic feature of these plots is that at larger distances the number of galaxies decreases. This phenomenon is entirely due to the way the surveys are built: they are flux-limited, therefore only the galaxies bright enough to have an apparent magnitude exceeding the survey cutoff are detected. At larger distances it is only possible to observe the intrinsically most luminous galaxies. To account for this incompleteness in the statistical analysis of these surveys, one needs to know the selection function (r), which basically provides the probability that a galaxy at a given distance r is included in the sample. This is the radial selection function that is usually estimated from the - previously calculated - luminosity function, (L). The luminosity function is defined by the number density of galaxies in a given range of intrinsic luminosity [L, L + dL], (L)dL. This function varies with morphological type, environmental properties and redshift due to galactic evolution. Traditionally it has been empirically fitted to a Schechter function [12]

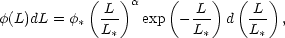(1)

where L_* is a characteristic luminosity which separates the faint galaxy range where the power-law with exponent dominates Eq. 1 and the bright end where the number density decreases exponentially.

Other selection effects affect the galaxy samples. Many of them are directional. Some are due to the construction of the sample: masks in given fields, fiber collisions in the spectrographs, etc. In addition, the sky is not equally transparent to the extragalactic light in all directions due to absorption of light performed by the dust of the Milky Way. Since the shape of our own Galaxy is rather flat, the more obscured regions are those with low values of | b| (where b is the galactic latitude). This effect has to be considered when computing the real brightness of a galaxy, which therefore depends on the direction of the line-of-sight. The best way to take this effect into account is to consider the well defined maps of the distribution of galactic dust [13].

For very deep samples, the absolute magnitude has to be estimated considering other adjustments like the K-correction, which takes into account that the luminosity of the galaxies at large redshift is detected at longer wavelength than actually was emitted.

Once the selection effects have been considered, the statistical analysis of the galaxy surveys are performed assigning to each galaxy a weight inversely proportional to the probability that the galaxy was included in the sample. A more clean solution is to consider volume-limited samples at the price of throwing away a huge amount of the collected data: At a given distance limit, one can easily calculate the absolute magnitude of a galaxy having the apparent magnitude limit of the survey. All galaxies intrinsically fainter that this absolute magnitude cutoff will be ignored in the volume-limited sample. An illustration of this procedure is shown in Fig. 3.

Figure 3. The left panel shows a region in the northern hemisphere of the CfA apparent magnitude limited sample. The apparent magnitude cutoff is m = 15.5. It contains nearly 5000 galaxies. The right panel shows the same region when considered volume-limited sample. Now only the 905 galaxies brighter than -19.70 + 5 log h has been included. The drop of the galaxy density with the distance to the observer (located at the vertex) appreciated in the left panel is not longer observed in the volume-limited sample.