3.2. (r) on recent samples

Fig. 5 shows the two-point correlation function in redshift space calculated on three different deep redshift surveys: LCRS [23], d2F (Hawkins et al. - the 2dFGRS team -, in preparation), and SDSS [24]. The agreement is quite remarkable, in fact the differences between LCRS and SDSS are mainly due to the fact that comoving distances have been calculated assuming different cosmological models. It is clear that trying to fit reasonably well a power-law (s) = (s / s₀)^- to the data is hopeless. In fact, the dotted lines show the real space correlation function calculated from the Automatic Plate Machine (APM) angular data [25] after deprojecting the angular correlation function with the Limber equation. Now, a reliable power-law (r) = (r/r₀)^-, with = 1.7 and r₀ = 4.1 h^-1 Mpc, can be fitted to the curves for scales r 4 h^-1 Mpc. The slope is in agreement with the results inferred by Zehavi et al. [24] for the SDSS early data: = 1.75±0.03 and r₀ = 6.1 ± 0.2 h^-1 Mpc, within the range 0.1 r 16 h^-1 Mpc. Although the APM amplitude was smaller, Baugh [25] reported an appreciable shoulder in (r) for scales 4 r 25 h^-1 Mpc where the correlation function was rising above the fitted power law. The diagram also illustrates the effects of the peculiar velocities in redshift surveys suppressing the short-range correlations and enhancing the amplitude at intermediate scales due to coherent flows [3, 4]. It is also interesting to note that the first zero crossing of the two-point correlation function occurs at scales around 30-40 h^-1 Mpc.

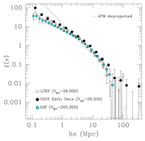Figure 5. The two-point redshift correlation function for the deepest available redshift surveys: The Las Campanas Redshift Survey [23], the 2dF (Hawkins et al. - the 2dFGRS team -, in preparation), and the early public release of the Sloan Digital Sky Survey [24]. The dotted lines, that fit well a power law, correspond to the real-space correlation function deprojected from the APM angular data using two different models of galactic evolution [25], (figure from Guzzo [4]).