A relativistic point particle is a zero dimensional object; the world line of such a particle, describing its time evolution, will be one dimensional and the standard quantum field theory (like QED) uses real and virtual world lines of particles in its description. In contrast, a string (at a given moment of time) will be described by an one dimensional entity and its time evolution will be a two dimensional world surface called the world sheet. The basic formalism of string theory - considered to be a possible candidate for a model for quantum gravity - uses a two dimensional world sheet rather than the one dimensional world line of a particle to describe fundamental physics. Since the point particle has been replaced by a more extended structure, string theory can be made into a finite theory and, in general, the excitations of the string can manifest as low energy particles. This provides a hope for describing both gauge theories and gravity in a unified manner. (For a text book description of string theory, see [41, 42]; for a more popular description, see [320, 321, 322]).
It was realized fairly early on that string theory can be consistently formulated only in 10 dimension and it is necessary to arrange matters so that six of these dimensions are compact (and very small) while the other four - which represents the spacetime - are presumably large and non compact. There is no fundamental understanding of how this comes about; but the details of the four dimensional theory depends on the way in which six extra dimensions are compactified. The simplest example corresponds to a situation in which the six dimensional geometry is what is known as calabi-yau manifold [323, 324, 325] and the four dimensions exhibit N = 1 supersymmetry. The current paradigm, however, considers different ten dimensional theories as weakly coupled limits of a single theory and not as inequivalent theories. Depending on the choice of parameters in the description, one can move from one theory to other. In particular, as the parameters are changed, one can make a transition from weakly coupled limit of one theory to the strongly coupled limit of another. These strong-weak coupling dualities play an important role in the current paradigm of string theories though explicit demonstration of dualities exists only for limited number of cases [326, 327, 328, 329].
The role of cosmological constant in string theories came into the forefront when it was realized that there exists a peculiar equivalence between a class of theories containing gravity and pure gauge theories. One example of such a duality [330] arises as follows: A particular kind of string theory in ten dimension (called type II B string theory) can be compactified with five of the dimensions wrapped up as 5-sphere (S5) and the other five dimensions taken to describe a 5-dimensional anti de Sitter spacetime with negative cosmological constant (AdS5). The whole manifold will then be S5 × AdS5 with the metric on the AdS sector given by
 |
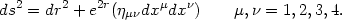(193) |
This string theory has an exact equivalence with the 4-dimensional
N = 4 supersymmetric
Yang-Mills theory. It was known for a long time that the latter theory
is conformally invariant; the large symmetry group of the
AdS5 matches precisely with the invariance group of
Yang-Mills theory. The limit
r 
is considered to be the
boundary of AdS space on which the dual field theory is
defined. This allows one to obtain a map from the string theory states
to the field which lives on the boundary. It must be stressed that it is
hard to prove directly the equivalence between type II B
AdS5 × S5 string theory and the
four dimensional Yang-Mills theory especially since we do not have a non
perturbative description of the former.
In this sense the Yang-Mills theory actually provides a definition of
the non perturbative type II B
AdS5 × S5 string theory. It is,
however, possible to verify the correspondence
by restricting to low energies on the string theory side.
If gravity behaves as a local field theory, then the entropy in
a compact region of volume R3 will scale as
S 
R3 while indications from
the physics of the horizons is that it should scale as
S
R2. One can provide a consistent
picture if gravity in D -dimensions is equivalent to a field
theory in D - 1 dimension with the entropy of the field theory
scaling as the volume of the D - 1 dimensional space which, of
course, is the same as the area in the original D -dimensional
space. This is achieved in a limited sense in the above model.
The AdS spacetime has a negative cosmological constant while the standard de Sitter spacetime has a positive cosmological constant. This change of sign is crucial and the asymptotic structure of these theories are quite different. We do not, however, know of any solution to string theory which contains de Sitter spacetime or even any solution to standard Einstien's equation with a positive cosmological constant. There are, in fact, some no-go theorems which state that such solutions cannot exist [331, 332, 333]. This, however, is not a serious concern since the no-go theorems assume certain positive energy conditions which are indeed violated in string theory.
If de Sitter solutions of the string theory exists, then it would be interesting to ask whether they would admit a dual field theory description as in the case of anti de Sitter space. Some preliminary results indicate that if such a duality exists, then it would be with respect to a rather peculiar type of conformal field theories [334, 335, 336]. The situation at present is reasonably open.
There is another indirect implication of the string theory paradigm for the cosmological constant problem. The detailed vacuum structure in string theory is at present quite unknown and the preliminary indications are that it can be fairly complicated. Many believe that the ultimate theory may not lead to a unique vacuum state but instead could lead to a set of degenerate vacua. The properties of physical theories built out of these vacua could be different and it may be necessary to invoke some additional criterion to select one vacuum out of many as the ground state of the observed universe. Very little is known about this issue [337] but advocates of anthropic principle sometimes use the possibility multiple degenerate vacua as a justification for anthropic paradigm. While this is not the only possibility, it must be stressed that the existence of degenerate vacua introduces an additional feature as regards the cosmological constant [338]. The problem arises from the fact that quantum theory allows tunneling between the degenerate vacua and makes the actual ground state a superposition of the degenerate vacua. There will be an energy difference between: (i) the degenerate vacua and (ii) the vacuum state obtained by including the effects of tunneling. While the fundamental theory may provide some handle on the cosmological constant corresponding to the degenerate vacua, the observed vacuum energy could correspond to the real vacuum which incorporates the effect of tunneling. In that case it is the dynamics of tunneling which will determine the ground state energy and the cosmological constant.
Acknowledgement
I thank J.S. Bagla, J.V. Narlikar, T. Roy Choudary and K. Subramanian for comments on the earlier version of the draft.