APPENDIX A. EMISSION-LINE CONTINUUM SUBTRACTION USING BROAD-BAND IMAGES

Some of the expressions derived in this appendix also appear in Waller (1990). Here we have carried out a more detailed analysis of the procedures used for flux-calibrating broad- or narrow-band imaging data. We have also considered the case that the field stars used for the normalization of the continuum image have absorption features in their spectra and considered the presence of other emission-lines in the galaxy spectrum (e.g. the [NII] 6548, 6584 ÅÅ doublet in our H filters) within the narrow-band filter used.

We consider two images, one taken with a narrow-band filter ( 100 Å; NB hereafter) and another taken with a broad-band one ( 1000 Å; BB hereafter). If we would be observing an astronomical object having a line in emission within the wavelength range of these filters, the total fluxes obtained (in counts after the sky subtraction) would be

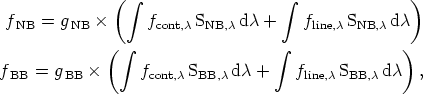(A1) (A2)

respectively for the NB and BB filters, where g_NB and g_BB are the ratios between counts and flux in ergs^-1cm^-2 (including exposure time, gain, system total efficiency, and atmospheric extinction), f_line, and f_cont, are the fluxes per unit wavelength (in units of erg s^-1 cm^-2 Å^-1) emitted by the object due to the line and the continuum, respectively, and S_line, and S_cont, are the normalized response functions of the NB and BB (including both the filter and detector efficiency), respectively.

Assuming that the continuum is approximately flat in the spectral region of both filters, we can write

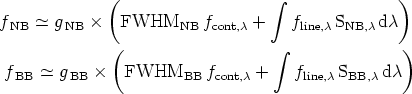(A3) (A4)

where FWHM is the Full Width at Half Maximum of the corresponding filter.

If we now consider that the width of the emission-line is significantly narrower that the NB filter (less that 1/10^th the FWHM_NB) we can simplify these expressions to

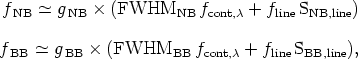(A5) (A6)

where f_line is the total flux of the emission line (in erg s^-1 cm^-2) and S_{NB, line} and S_{BB, line} are the normalized responses of the filters at the wavelength of the emission line.

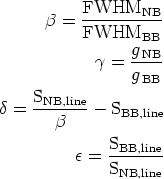
Then, defining

(A7) (A8) (A9) (A10)

we obtain f_line, f_cont,, and the equivalent width of the line (EW) as

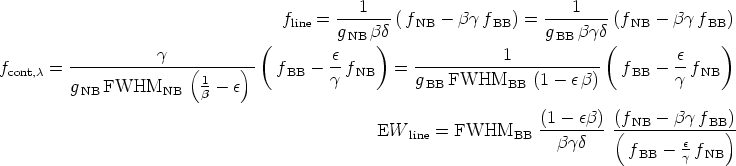(A11) (A12) (A13)

In order to solve these equations (and obtain the pure emission-line image of the object) we need to determine the , , , and parameters. The , , and parameters can be easily obtained from the normalized response function of the NB and BB filters given the rest-frame wavelength of the emission-line considered and the recession velocity of the object.

With regard to the parameter two approaches can be followed. First, we can determine the value of the parameter if both the NB and BB images are flux-calibrated just dividing the corresponding calibration factors. However, this parameter can be also measured without flux-calibrating any of the two images. In this sense, we can measure the total counts on both images for a large number of objects with well-known spectral properties in the wavelength range of interest. In the case of the line equivalent width, it is not necessary either to calibrate any of the images since Equation A13 does not depend on g_NB or g_BB. On the other hand, if we are interested in deriving the emission-line flux (or the continuum flux) of the object at least one of the images should be flux-calibrated.

Thus, with regard to the derivation of , if we measure the total counts on both the NB and BB for a number of featureless objects (usually field stars) we get

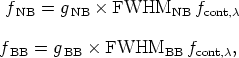(A14) (A15)

which leads to

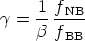(A16)

This is the most commonly used method for subtracting the continuum contribution in narrow-band images. This method is particularly simple and powerful because the f_NB / f_BB ratio (= × ) can be used to scale the BB image to the NB one and obtain a pure emission-line image without any previous knowledge about the filters response functions.

In addition, in some cases it is not possible to find featureless stars usually because the emission-line of interest (or other lines) are present in absorption (or emission) in their spectra. In that case the Equation A16 has to be substituted by

(A17)

where the sum is extended to the number of features present in the field stars spectra (equivalent widths would be negative in absorption and positive in emission).

The values determined for , (or the × product) would allow to obtain the continuum-subtracted image. However, if we intend to calibrate the resulting image resolving f_line in Equation A11 we have to previously derive g_NB or g_BB. The observation of several spectrophotometric standards stars would allow to obtain the following relation

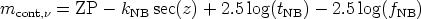(A18)

where ZP is the zero point of the calibration, k_{, line} is the extinction coefficient for the NB filter, t_NB is the exposure time of the NB image, and m_cont, is the monochromatic magnitude (see e.g. Hamuy et al. 1992), which is related with the flux via

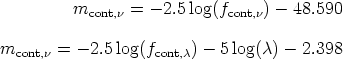(A19) (A20)

where f_cont, is expressed in erg s^-1 cm^-2 Hz^-1, f_cont, in erg s^-1 cm^-2 Å^-1, and is in Å.

Thus, once the ZP and k_NB coefficients are obtained from the Bouger-line fit to the spectrophotometric standards data we can obtain the conversion factor g_NB from Equations A14, A18, and A20 as

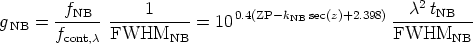(A21)

and, then

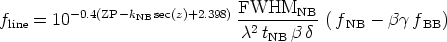(A22)

On the other hand, in the case that only the broad-band image is flux calibrated we obtain

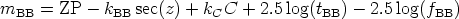(A23)

where k_BB is the extinction coefficient for the BB filter, C and k_C are the color and color coefficient for a particular color term, and t_BB is the exposure time for the BB image. Since m_BB is also expressed as

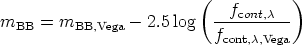(A24)

we derive g_BB using

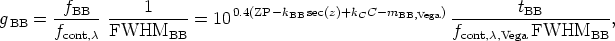(A25)

which finally leads to the flux of the emission line

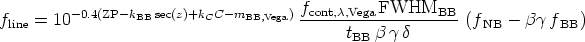(A26)

In those cases where both photometric and spectrophotometric calibrators are available the comparison of the g_NB / g_BB ratio with the right side of Equation A16 should provide an additional test for the reliability of the spectral response functions assumed for the NB and BB filters. In our case the differences derived between these two values were of the order of 5 per cent.

Finally, it is important to take into account the contribution that other emission lines could have to the fluxes and equivalent widths derived using Equations A1, A22, A26, and A13. Although the terms due to these other lines (typically the doublet [NII] 6548, 6584 ÅÅ for observations in the light of H) are not included in Equations A1 and A2 their contribution can be corrected by considering that f_line, as it appears in these equations, can be defined in a way that

(A27)

where f'_line and f'_j are the corrected fluxes for the line of interest and those other lines included in the filter, respectively, and the sum in the index j is extended to all contaminating lines but not the line of study. If we now consider the line ratios between the contaminating lines and the line of interest given by spectroscopy observations,

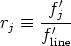(A28)

we obtain

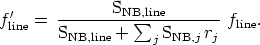(A29)

This expression and the corresponding correction of the EW_line are valid as long as the contribution of the contaminating lines to the flux within the BB filter is negligible.