


Given the results from observational cosmology discussed in the previous two sections we are now able to present a concrete picture of the universe, as opposed to the traditional array of models with very different properties. Taking a more comprehensive view, in Table 2 we present a set of cosmological parameters (without errors) that might be taken as the "best estimates" based on various observational and theoretical studies. [37]
This set of parameters describes a flat universe the dynamics of which is dominated by two mysterious forms of energy, most prominently, the cosmological constant. So then, the long-standing debate over whether or not the cosmological term should be included in Einstein's theory is over; not only should it be included, it dominates the universe. Although the debate over the existence of the cosmological constant has ended, the debate over its physical implications has just begun. Further comments about this debate will be discussed in the conclusion.
| Parameter | Value | Primary Sources |
| Hubble constant | H0 = 72 km . s-1 . Mpc-1 | [13] |
| Cosmological Constant |   = 0.70 = 0.70 |
[16, 33] |
| Matter |  m = 0.30 m = 0.30 |
[16, 33] |
| Baryonic matter |  b = 0.04 b = 0.04 |
[33] |
| Dark matter |  CDM = 0.26 CDM = 0.26 |
theory: Eq. (61) |
| Curvature |  k = 0.00 k = 0.00 |
[16, 20-22, 33] |
| Deceleration parameter | q0 = - 0.55 | theory: Eq. (39) |
The other mysterious form of energy listed in
Table 2,
 CDM,
is dark matter where "CDM" stands for "cold dark matter." Recall
that ordinary matter made up of atomic nuclei only contributes to the
baryon content of the universe with
CDM,
is dark matter where "CDM" stands for "cold dark matter." Recall
that ordinary matter made up of atomic nuclei only contributes to the
baryon content of the universe with
 b
b
 0.04. However, since
the total matter content is
0.04. However, since
the total matter content is
 m
m
 0.30, the rest of the
matter in the universe must be in some exotic, unseen form which is why
we call it dark matter
0.30, the rest of the
matter in the universe must be in some exotic, unseen form which is why
we call it dark matter
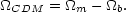 |
(61) |
We have known about dark matter for several decades now, having been first discovered through anomalous rotation curves of galaxies. [3] The results from the CMB anisotropies only help to confirm that not only does dark matter exist, but that it comprises roughly 90% of the matter in the universe.
Given values of the cosmological parameters, we can now solve for the dynamics of the universe. The Friedmann equations (16) and (17) for our present universe (pm = 0, k = 0) can be combined to give
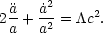 |
(62) |
This equation can be solved exactly giving the result [38]
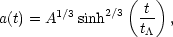 |
(63) |
where A =  m,
0 /
m,
0 /

 , 0
, 0
 0.43 and
t
0.43 and
t = (4/3
= (4/3
 c2)1/2
c2)1/2
 3.4 × 1017 s. The cosmic scale
factor is plotted in Fig. 5 and compared to the
purely de Sitter
universe described by Eq. (20). From this comparison, we see that,
today, the qualitative behavior of our universe is that of a de Sitter
universe except that the presence of matter has caused the universe to
expand less than in the de Sitter case.
3.4 × 1017 s. The cosmic scale
factor is plotted in Fig. 5 and compared to the
purely de Sitter
universe described by Eq. (20). From this comparison, we see that,
today, the qualitative behavior of our universe is that of a de Sitter
universe except that the presence of matter has caused the universe to
expand less than in the de Sitter case.
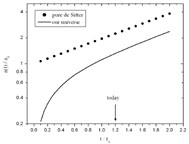 |
Figure 5. The cosmic scale factor for our universe compare to the de Sitter model. |
With a(t) in hand, we can now write a precise metric for the universe
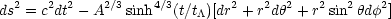 |
(64) |
This tells us that we can visualize the universe as an expanding Euclidean sphere with the expansion governed by a(t) as given in Eq. (63). Note, however, that in this visualization the universe is represented as the entire volume of the sphere and not just the surface.
Another interesting feature that emerges from this picture is that if
 is truly
constant, the universe would have once been
matter-dominated. To see why this is, recall that because the size of
the universe changes, the density parameters are functions of time. As
we go back in time, the universe gets smaller so that the energy
density of matter
is truly
constant, the universe would have once been
matter-dominated. To see why this is, recall that because the size of
the universe changes, the density parameters are functions of time. As
we go back in time, the universe gets smaller so that the energy
density of matter
 m
gets larger while the energy density
associated with
m
gets larger while the energy density
associated with  ,
see Eq. (15), remains constant. Using
Eq. (22) we can see that the ratio of matter-to-cosmological constant is
,
see Eq. (15), remains constant. Using
Eq. (22) we can see that the ratio of matter-to-cosmological constant is
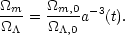 |
(65) |
Therefore, at some finite time in the past the universe was such that
 m /
m /

 > 1. Since the expansion of a
matter-dominated universe would be decelerating, this implies that the
universe underwent a transition from decelerated expansion to
accelerated expansion. This behavior is reflected in the deceleration
parameter as a function of time, which, given the current cosmological
parameters becomes
> 1. Since the expansion of a
matter-dominated universe would be decelerating, this implies that the
universe underwent a transition from decelerated expansion to
accelerated expansion. This behavior is reflected in the deceleration
parameter as a function of time, which, given the current cosmological
parameters becomes
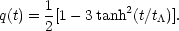 |
(66) |
Figure 6 is a plot of q(t) and
shows that the deceleration parameter was
once positive and that a transition to q(t) < 0
occurred around the time at which
 m /
m /

 = 1.
= 1.
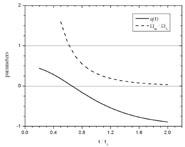 |
Figure 6. The deceleration parameter of our
universe. The sign of q(t)
switches from positive to negative at around the same time that the
universe goes from matter-dominated to
|
Having a specific model of the universe allows us to determine specific answers to questions that cosmologists have been asking for decades. While we cannot address all such questions in this paper we will tackle a few of the most common: (a) What is the age of the universe? (b) Will the universe expand forever or will the expansion eventually stop followed by a re-collapse? (c) Where is the edge of the observable universe?
The age of the universe can be calculated by integrating dt from now,
z = 0, back to the beginning
z =  . For our
universe, the steps leading to Eq. (36) produces
. For our
universe, the steps leading to Eq. (36) produces
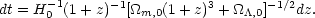 |
(67) |
Making the definition
x  1 + z,
the present age of the universe is given by
1 + z,
the present age of the universe is given by
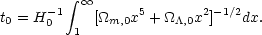 |
(68) |
The solution to Eq. (68) is complex. Taking only the real part gives
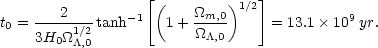 |
(69) |
The question of whether or not the universe will expand forever is
determined by the asymptotic behavior of a(t).
Since sinh(x) diverges as
x 
 ,
it is clear that the universe will continue to
expand indefinitely unless some presently unknown physical process
drastically alters its dynamics.
,
it is clear that the universe will continue to
expand indefinitely unless some presently unknown physical process
drastically alters its dynamics.
Finally, concerning the question of the size of the observable universe, there are two types of horizons that might fit this description, the particle horizon and the event horizon. The particle horizon is the position of the most distant event that can presently be seen, that is, from which light has had enough time to reach us since the beginning of the universe. Unfortunately, since current evidence suggests that the universe was not always dominated by the cosmological constant, we cannot extend the current model back to the beginning. We can, however, extend it into the future. The event horizon is the position of the most distant event that we will ever see. If we consider a photon moving radially toward us from this event, then Eq. (31) describes its flight. Since we are interested in those events that will occur from now t0, onward, Eq. (31) leads to
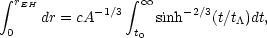 |
(70) |
where rEH is the radial coordinate of our event horizon. Performing a numerical solution to the integral yields
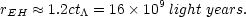 |
(71) |
This result suggests that 16 billion light years is the furthest that we will ever be able to see. As far as we are aware, the most distant object ever observed (besides the CMB) is currently the galaxy RD1 at a redshift of z = 5.34, which places it approximately 12.2 billion light years away. [39]