4. THE BARYONIC DENSITY

The ratio of baryons to photons or the baryon abundance is defined as

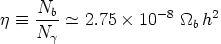(16)

where N_b is the number density of baryons and N = 4.11 × 10⁸ m^-3 is the number density of photons. Thus the primordial abundances of baryonic matter in the standard Big Bang nucleosynthesis scenario (BBN) is proportional to _b h². Its value is obtained in direct measurements of the abundances of the light elements ⁴He, ³He, ²H or D, ⁷Li and indirectly from CMBR observations and galaxy cluster observations.

If the observed abundances are indeed of cosmological origin, they must not significantly be affected by later stellar processes. The helium isotopes ³He and ⁴He cannot be destroyed easily but they are continuously produced in stellar interiors. Some recent helium is blown off from supernova progenitors, but that fraction can be corrected for by observing the total abundance in hydrogen clouds of different age, and extrapolating it to time zero. The remainder is then primordial helium emanating from BBN. On the other hand, the deuterium abundance can only decrease, it is easily burned to ³He in later stellar events. The case of ⁷Li is complicated because some fraction is due to later galactic cosmic ray spallation products.

Among the light elements the ⁴He abundance is easiest to observe, but also least sensitive to _b h², its dependence is logarithmic, so that only very precise measurements are relevant. The best "laboratories" for measuring the ⁴He abundance are a class of low-luminosity dwarf galaxies called Blue Compact Dwarf (BCD) galaxies, which undergo an intense burst of star formation in a very compact region. The BCDs are among the most metal-deficient gas-rich galaxies known. Since their gas has not been processed during many generations of stars, it should approximate well the pristine primordial gas.

Over the years the observations have yielded many conflicting results, but the data are now progressing towards a common value [27], in particular by the work of Yu. I. Izotov and his group. The analysis in their most recent paper [28], based on the two most metal-deficient BCDs known, gives the result

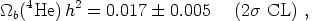(17)

where the error is statistical only. Usually one quotes the ratio Y_p of mass in ⁴He to total mass in ¹H and ⁴He, which in this case is 0.2452 with a systematic error in the positive direction estimated to be 2-4%. Because of the logarithmic dependence, this error translated to _b h² could be considerable, of the order of 100% .

The ³He isotope can be seen in the Milky Way interstellar medium and its abundance is a strong constraint on _b h². The ³He abundance has been determined from 14 years of data by Balser et al. [29]. More interestingly, Bania et al. [30] combined Milky Way data with the helium abundance in stars [31] to find

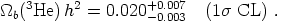(18)

There are actually three different errors in their analysis, and their quadratic sum gives the total error. The first error is from the observed emission-line that includes the errors in the Gaussian fits to the observed line parameters. The second error is from the standard deviation of the observed continuum data and the third error is the percent uncertainty of all models that have been used in the analyses of reference [29].

For a constraint on _b h² from ⁷Li, Coc et al. [32] update the previous work of several groups. More importantly, they include NACRE data [33] in their compilation, and the uncertainties are analysed in detail. There is some lack of information about the neutron-induced reaction in the NACRE compilation, but the main source of uncertainty for the lighter neutron-induced reaction (e.g. ¹H(n, )²H and ³He(n, p)³H) is the neutron lifetime (for the present value see the Review of Particle Physics [34]). However, there is no new information about the heavier neutron-induced reaction (e.g. ⁷Li) or for ³He(d, p)³He, but in this compilation the Gaussian errors have been opted from the polynomial fit of Nollett & Burles [35]. We quote Coc et al. [32] for

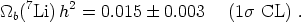(19)

The strongest constraint on the baryonic density comes from the primordial deuterium abundance. Deuterium is observed as a Lyman- feature in the absorption spectra of high-redshift quasars. A recent analysis [36] gives

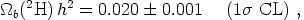(20)

more precisely than any other determination. Some systematic uncertainties remain in the calculations arising from the reaction cross sections.

Very recently Chiappini et al. [37] have redefined the production and destruction of ³He in low and intermediate mass stars. They also propose a new model for the time evolution of deuterium in the Galaxy. Taken together, they conclude that _b h² 0.017, in good agreement with the values in Eqs. (18) and (20).

Let us now turn to the information from the cosmic microwave background radiation and from large scale structures. There are many analyses of joint CMBR data, in particular three large compilations. Percival et al. [38] combine the data from COBE-DMR [1] MAXIMA [39], BOOMERANG [40], DASI [6], VSA [5] and CBI [4] with the 2dFGRS LSS data [17]. Wang et al. [41] combine the same CMBR data (except VSA) with 20 earlier CMBR power spectra, take their LSS power spectra from the IRAS PSCz survey [15], and include constraints from Lyman forest spectra [42] and from the Hubble parameter [9] quoted in Eq. (15). Sievers et al. [43] also use the same CMBR data as Percival et al. [38] (except VSA), combine them with earlier LSS data, and use the HST Hubble parameter [9] quoted in Eq. (15) and the supernova data referred to in Section 5 as supplementary constraints. All these analyses are maximum likelihood fits based on frequentist statistics, so the use of the Bayesian term "prior" for constraint is a misnomer.

Assuming that the initial seed fluctuations were adiabatic, Gaussian, and well described by power law spectra, the values of a large number of parameters are obtained by fitting the observed power spectrum. Here we shall only discuss results on _b h² which is essentially measured by the relative magnitudes of the first and second acoustic peaks in the CMBR power spectrum, returning to this subject in more detail in Section 6.

The data used in the three compilations are overlapping but not identical, and the central values show a spread over ± 0.0003. This we treat as a systematic error to the straight unweighted average of the central values. Two compilations [38], [41] consider models with and without a tensor component. Since the fits are equally good in both cases we take their difference, ± 0.0008, to constitute another systematic error. We shall use this averaging prescription also in Section 6 to obtain values of other parameters. All the analyses can then be summarized by the value

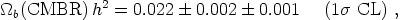(21)

where the statistical error corresponds to references [38], [41].

Table 1: The baryonic density parameter

Method		b h2	Error	References
4He abundance	4.7 +1.0-0.8 × 10-10	0.017 ± 0.005	2 stat. only	[28]
3He abundance	5.4 +2.2-1.2 × 10-10	0.020 +0.007-0.003	1 stat. only	[30]
7Li abundance	5.0 × 10-10	0.015 ± 0.003	1 stat. only	[32]
2H abundance	5.6 ± 0.5 × 10-10	0.020 ± 0.001	1 stat.+syst.	[36]
CMBR + 2dFGRS	---	0.022 ± 0.002 ± 0.001	1 stat.+ syst.	[38] [41]

In Table 1 we summarize the results from Eqs. (17-21). From this table one can conclude that all determinations are consistent with the most precise one from deuterium [36]. A weighted mean using the quoted errors yields 0.0194 ± 0.0008 which is dominated by deuterium. However, all light element abundance determinations generally suffer from the potential for systematic errors. As to CMBR, the statistical errors quoted in all compilations have been obtained by marginalizing, so they are certainly unrealistically small. We take a conservative approach and add a systematic error of ± 0.002 linearly to each of the five data values before averaging. The weighted mean is then

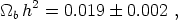(22)

in excellent agreement with all the uncorrected input values in Table 1.

One further source of _b information is galaxy clusters which are composed of baryonic and non-baryonic matter. The baryonic matter takes the forms of hot gas emitting X-rays, stellar mass observed in visual light, and perhaps invisible baryonic dark matter of unknown composition. Let us denote the respective fractions f_gas, f_gal, and f_bdm. Then

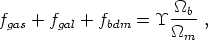(23)

where describes the possible local enhancement or diminution of baryon matter density in a cluster compared to the universal baryon density. This relation could in principle be used to determine _b when one knows _m (or vice versa), since f_gas and f_gal can be measured, albeit with large scatter, while f_bdm can be assumed negligible. Cluster formation simulations give information on [44], [45] to a precision of about 10%. However, the precision obtained for _b h² by adding several 10% errors in quadrature does not make this method competitive.