3. GLOBAL STAR FORMATION IN DISKS

Disk star formation can be understood via a hybrid model that is a combination of phenomenology and gravitational instability theory. The low efficiency of star formation is determined by the gravitational instability of a cold gas-rich disk, resulting in the formation of warm molecular gas clouds which in turn fragment into stars. Cloud collapse and star formation are enhanced by cloud coalescence and growth, as the clouds orbit the galaxy. This process is modulated and amplified by the spiral density wave pattern of the differentially rotating disk. The instability in a gas disk is quenched by the Toomre criterion, when the Toomre parameter, Q µ_crit / µ_gas, becomes larger than unity. Here the critical surface density is, to within a numerical factor of order unity, given by _gas/G with equal to the epicyclic frequency and _gas being the gas velocity dispersion. For a disk consisting of stars and gas, the criterion must be slightly modified, but it is essentially the coldest component, the gas, that drives the instability, provided that the gas surface density µ_gas µ_{* g} / _*, where µ_* is the disk stellar surface density and _* is the stellar velocity dispersion.

This scheme is used to derive an empirical star formation rate, the Schmidt-Kennicutt law, which has been applied to fit a large sample of star-forming disk galaxies. Beyond the radius where the azimuthally-averaged surface density drops below the critical value, the disk is stable to cloud formation. The inferred star formation rate, if one assumes that the clouds once formed are unstable to star formation within a disk rotation time or less, can be approximated by

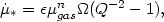for Q < 1, with n 1. The instability requires the disk to be in differential rotation, at rate (r).

The predictions of such a semi-empirical model are straightforward: star formation occurs inside-out in disks, quenching below the threshold surface density of cold gas (HI or H₂) of a few solar masses per square parsec, and star formation decays monotonically as the gas supply is exhausted. The duration of star formation can be extended if gas infall occurs from the halo.

Broadly viewed, such a model works reasonably well from the point of view of chemical evolution (cf. Prantzos, these proceedings). However detailed recent studies of disk star formation suggest that there are significant omissions in the underlying physics. For example, there is the realization that the radial dependence of disk star formation is not always well modeled by the empirical law [Ferguson et al.1998]. In some galaxies, star formation occurs below the threshold surface density. This is most likely due to the non-axially symmetric distribution of the gas. Locally the gas surface density may be high, as for example in spiral arms.

Another hint of the need for a more complex theory comes from studies of the age distribution of disk stars. In the Milky Way, the star formation rate history is seen to be non-monotonic [Rocha-Pinto et al.2000]. In fact, studies of chromospheric age indicators reveal a series of modest star bursts. A similar pattern is found in other nearby galaxies where stars can be resolved, and the Hertzsprung-Russell diagram can be used to study the star formation history. Presumably, infall is occurring in a non-uniform way, for example via mergers of satellite galaxies. Studies of the metallicity distribution of old disk stars in the solar neighbourhood require early infall in order to account for the paucity of old metal-poor stars.

The underlying logic of dissipative disk formation in weakly interacting halos of cold dark matter seems compelling. Star formation is inefficient in disks because of self-regulation. The disk forms via collapse in the dark halo of gas that has acquired some angular momentum via tidal torques between neighbouring halos. The dimensionless angular momentum parameter is initially v_rot / 0.15, and contraction by a factor of order 10 in an isothermal dark halo of virial radius 100 kpc that dominates the gravity results in a disk of scale around 5 kpc if specific angular momentum is approximately conserved.

The gas disk is cold and gravitationally unstable, forming giant cloud complexes that aggregate gas and are in turn unstable to fragmentation. Feedback both via dynamical heating of the stars and by supernova remnant interactions heat and stabilize the system against further star formation, until further gas infall drives further gas cooling.

Because of the bottom-up nature of the clustering hierarchy, driven by the approximately scale-invariant primordial density fluctuation spectrum, the density fluctuation amplitude scales with mass as / (1 + z)^-1M^-(n+3)/6 with n - 1.5 on galaxy scales. This means that massive halos form after lower mass halos, with the virialization redshift scaling as approximately M^-1/4. 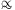There is as much mass in the low mass halos as in the massive halos, with the number of halos scaling as dN/dM M^-2.

There are serious deficiencies in the model that remain when disk formation is incorporated by such simple rules into semi-analytic galaxy formation theory that builds on numerical simulations of dark matter clusters.