6. ANALYTIC DISK GALAXY FORMATION

The brute force computational approach will not resolve the outstanding problems in disk galaxy formation. What seems to be needed are further analytical insights that will allow refinement of the simple prescriptions for star formation. One such approach has come from studying turbulence-driven viscous evolution of differentially rotating disks. Recent investigations of star formation suggest that turbulence plays an important role in accounting for the longevity of star-forming clouds and their fragmentation into stars. The Jeans mass in a typical interstellar cloud greatly exceeds the stellar mass range. It is likely that the gravitational instability of galaxy disks is a primary source of interstellar cloud turbulent motions, supplemented on small scales by supernova feedback. Of course, these drivers of turbulence are coupled together, since the rates of star formation and star deaths are controlled by global gravitational instability. In effect, differential rotation is the ultimate source of the turbulence.

A promising hypothesis is that turbulent viscosity, by regulating the gas flow, controls the star formation rate, and indeed that the star formation time-scale is given by the time-scale for the viscous transfer of angular momentum [Silk and Norman1981]. On the scale of molecular clouds, such an ansatz is reasonable, since one has to shed angular momentum in order to form stars. Magnetic fields are the common culprit in conventional star-forming clouds, but in protogalactic disks one most likely has to appeal to another source of angular momentum transfer. Turbulent viscosity is capable of fulfilling this role. Indeed, the resulting disk has been shown to generically develop an exponential density profile [Lin and Pringle1987]. In infall models, the initial angular momentum profile determines the final disk scale length if angular momentum is conserved. However as found in high resolution simulations, some 90 percent of the baryonic specific angular momentum is lost to the dark halo, and there is no preferred solution for disk sizes. In viscous disk models, the scale length is set by the competition between viscosity-driven star formation, that freezes the scale length once stars form, and dynamical friction on the dark matter, that competes for the same angular momentum supply. The characteristic viscous scale is determined by the cloud mean free path between collisions, itself comparable to the disk instability scale that drives the turbulence, and in combination with the residual rotation rate, provides the ultimate constraint on disk scales.

Another byproduct of the viscous disk model is the gas fraction [Silk2001]. The viscous redistribution time-scale, and hence the star formation time-scale, is

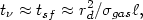where is the cloud mean free path (of order the disk scale height), and _gas is the cloud velocity dispersion. Disk instability yields _gas . The star formation efficiency, if determined by supernova feedback and approximate conservation of momentum, is _gas / v_SN, where v_SN is the specific supernova momentum per unit mass injected into the interstellar medium. Here v_SN E_SN / m_SNv_c, where m_SN is the mass in stars per supernova and v_c is the velocity of transition of a remnant to approximate momentum conservation. The characteristic star formation time may then defined to be

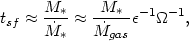where (r) is the disk rotation rate at radius r, M _* (r) is the instantaneous stellar mass and M_gas is the gas mass. A steady state is reached in which the gas fraction is

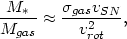and the disk scale length is

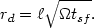Thus the disc scale depends both on cosmology and on local conditions.

The inferred present epoch numbers are plausible: for M _* 6 × 10¹⁰ M, one finds _* 3M / yr and M_gas / M_* 0.1. Also, one has now _gas 10 km s^-1, v_SN 1000 km s^-1, and 0.3kpc. At disk formation, one expects that M_gas / M _* 1, t_sf 10⁹ yr, and 1 kpc, appropriate to the protodisk. These values result in a stellar disk scale-length r_d 3 kpc. It is encouraging that simple analytic estimates come out with reasonable numbers for gas and stellar disk scales and gas fraction. Whether such a simple model survives incorporation into 3-dimensional simulations of disk formation in the presence of a live dark matter halo and energetic winds remains of course to be seen.