


In a CDM universe, the formation of cosmic structures is
governed by gravitational processes. At large scales
the influence of baryons is negligible. Starting from a Gaussian
density fluctuation field with a given processed power spectrum,
the gravitational clustering of the fluctuations is followed to
the present epoch by means of cosmological N-body simulations,
and the results are confronted with observations (for recent numerical
results see e.g.,
Jenkins et al. 1998;
Evrard et al. 2002).
The completion of large surveys of galaxies and clusters of galaxies,
the measurements of sub-degree anisotropies in the microwave
background radiation, and the detection of cosmological SNe
improved significantly our understanding of the large-scale structure
and the mass-energy composition of the Universe (for a recent review see
Guzzo 2002
and the references therein). The agreement between observations and
the CDM predictions is remarkable (see Frenk, this volume).
The "concordance"
 CDM cosmological
model
(Bahcall et al. 1999)
emerges as the favorite one. For this model, the universe is flat with
the following approximate values of the cosmological parameters:
CDM cosmological
model
(Bahcall et al. 1999)
emerges as the favorite one. For this model, the universe is flat with
the following approximate values of the cosmological parameters:
 bar = 0.04,
bar = 0.04,
 CDM =
0.26,
CDM =
0.26, 
 = 0.7,
= 0.7,
 8 = 0.9, and
H0 = 65 km s-1 Mpc-1. In this
review, with the generic term CDM we will refer to the
8 = 0.9, and
H0 = 65 km s-1 Mpc-1. In this
review, with the generic term CDM we will refer to the
 CDM model.
CDM model.
At the scales of galaxies and clusters of galaxies, where high resolution is required in the simulations, an extensive work on formation, mass function, structure, and evolution of the CDM matter halos has been done in the last decade. Analytical and semi-analytical approaches, but mainly numerical N-body simulations, were used. The dark halos are the backbone of the galaxy formation models. Following, we discuss some results which appear relevant for the properties of galaxies:
i) The shape of the mass function of CDM halos is approximately similar to that of the observed Schechter luminosity function of galaxies (e.g., Press & Schechter 1974; Lacey & Cole 1993). The semi-analytical models show that the main problem is at the faint end of the luminosity function (e.g., Kauffmann et al. 1993; Cole et al. 2000; Somerville & Primack 1999); however, reionization and feedback may possibly solve the conflict (Benson et al. 2002a, see also this volume).
ii) The average density profile of CDM halos is described
typically by a universal two-parameter profile, both parameters
depending ultimately only on the halo mass
(Navarro, Frenk, &
White 1997,
hereafter NFW).
Less massive halos tend to be more concentrated than the more massive ones.
However, for a given mass, the halo density profiles show a scatter around
the NFW profile. This scatter correlates with the halo mass aggregation
history (MAH), in the sense that halos assembled earlier are more
concentrated
(Avila-Reese et al. 1998,
1999;
Wechsler et al. 2002).
Some dependence on the environment has also been reported (but see
Lemson & Kauffmann
1999).
The CDM halos are too concentrated and their
inner density profiles are cuspy, in apparent disagreement with
observations, mainly the inner rotation curves of dwarf and LSB galaxies
(Moore 1994;
Burkert 1995;
see also Bosma, de Blok, and Colín et al.
in this volume). At galaxy-cluster scales, the inferred halo inner density
profiles, under the uncertainties, typically are fitted by both the NFW and
the pseudo-isothermal profiles.
Observations seem to show that, from dwarf to galaxy-cluster scales, the
central halo density is poorly dependent on mass, and the core radius
increases roughly proportional to the maximum circular velocity
Vmax
(Firmani et al. 2000,
2001).
Figure 1 presents the approximate range
of values of the halo central density and core radius vs. Vmax
inferred from observations.
Another potential problem of the CDM halos is that the number of subhalos
within MW-sized halos overwhelms the number of observed satellite
galaxies by a large factor
(Kauffmann et al. 1993;
Klypin et al. 1999;
Moore et al. 1999).
Besides, the large population of satellite subhalos could have
a dramatic effect on the dynamics of the galaxy disks
(Moore et al. 1999;
Colpi, Mayer &
Governato 1999).
Owing to the success of the CDM model at large scales, only minor
modifications to the model have been proposed in order to solve these
potential problems. For example, in a Warm Dark Matter (WDM) scenario
with particle masses of
~ 0.6 - 1 KeV, the satellite velocity function in
MW-sized halos is well reproduced, while at larger scales the predictions
are similar to CDM
(Colín et al 2000).
However, the inner
density profiles of galaxy-sized and larger halos are similar to their CDM
counterparts; even the small subhalos show density profiles well
fitted by the NFW profile, although with concentrations lower than
predicted by CDM
(Avila-Reese et al. 2001;
Bode, Ostriker & Turok 2001).
Conversely, self-interacting dark matter (SIDM) with a velocity-dependent
cross sections,
 DM = 0.5 -
1.0 (100 km s-1 /
Vmax) cm2 / gr,
produces inner halo density profiles in agreement with observations
at all scales (Fig. 1), but the substructure
remains similar to CDM
(Firmani et al. 2001;
Colín et al. 2002,
see also this volume).
The substructure problem may be actually alleviated by the reionization,
which certainly has to be taken into account in the formation of dwarf
galaxies
(Bullock et al. 2000;
Benson et al. 2002a).
DM = 0.5 -
1.0 (100 km s-1 /
Vmax) cm2 / gr,
produces inner halo density profiles in agreement with observations
at all scales (Fig. 1), but the substructure
remains similar to CDM
(Firmani et al. 2001;
Colín et al. 2002,
see also this volume).
The substructure problem may be actually alleviated by the reionization,
which certainly has to be taken into account in the formation of dwarf
galaxies
(Bullock et al. 2000;
Benson et al. 2002a).
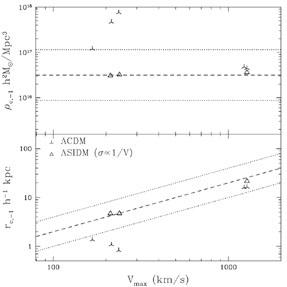 |
Figure 1. Central density and core radius
in this plot are defined
as the density and radius where the halo profile slope becomes
steeper than -1. The dotted lines encompass roughly the
2 |
iii) The angular momentum distribution in most of CDM halos
seems to be well parametrized by a universal function, and the disks formed
within them, assuming detailed angular momentum conservation, are roughly
exponential
(Bullock et al. 2001b).
The global spin parameter
 has a
lognormal distribution and is approximately independent of the
cosmology, mass, and environment (e.g.
Catelan & Theuns
1996).
Two mechanisms for the origin of the halo angular momentum seem to compete:
linear tidal torques and orbital angular momentum transfer of merging
satellites (e.g.,
Peebles 1969;
Vitvistkaya et al. 2002;
Maller, Dekel &
Somerville 2002).
The role of angular momentum in formation of galaxies is crucial.
More work should be done, for example, on the symmetry and degree of
alignment of the angular momentum distribution in the halos (see
van den Bosch et
al. 2002
for recent results) and on the angular momentum dependence on environment.
has a
lognormal distribution and is approximately independent of the
cosmology, mass, and environment (e.g.
Catelan & Theuns
1996).
Two mechanisms for the origin of the halo angular momentum seem to compete:
linear tidal torques and orbital angular momentum transfer of merging
satellites (e.g.,
Peebles 1969;
Vitvistkaya et al. 2002;
Maller, Dekel &
Somerville 2002).
The role of angular momentum in formation of galaxies is crucial.
More work should be done, for example, on the symmetry and degree of
alignment of the angular momentum distribution in the halos (see
van den Bosch et
al. 2002
for recent results) and on the angular momentum dependence on environment.
iv) The hierarchical mass aggregation history (MAH) of CDM
halos scatters around its average, because they emerge from a stochastic
density field. On average, the less massive halos tend to assemble a
given fraction of their mass at earlier epochs than the more massive halos
(Avila-Reese et al. 1998).
The halos may grow by a variety of merging regimes going from smooth
mass accretion to violent major mergers (e.g.,
Salvador-Solé et
al. 1998).
This variety of merging regimes is relevant to the morphology of the
galaxies formed within the halos. Cosmological simulations show that (i)
most of the z = 0 galaxy-sized halos are not contained within
larger halos nor have
close massive companions, and that (ii) most of the mass of these halos has
been aggregated by smooth accretion
(Avila-Reese et al. 1999;
Somerville & Kolatt
1999;
Gottlöber et
al. 2001).
Nevertheless, the pair abundance and the major merger rate increase with
z, and this increase is faster for cluster halos than for field
halos
(Gottlöber et
al. 2001).
The predicted major merging rates agree with
those inferred from accurate statistics of galaxy pairs. From the fraction
of normal galaxies in close companions (with separations less than
50 kpch-1) inferred from observations
at z = 0 and z = 0.3
(Patton et al. 2000,
2002),
and assuming an average
merging time of ~ 1 Gyr, we estimate that the major merging rate at the
present epoch is ~ 0.01 Gyr-1 for halos in the range of
0.1 - 2.0 1012
M , while at
z = 0.3 the rate increased to
~ 0.018 Gyr-1. These values are only slightly lower than
predictions for the
, while at
z = 0.3 the rate increased to
~ 0.018 Gyr-1. These values are only slightly lower than
predictions for the
 CDM model,
suggesting that the model can be used to predict
the increasing merging rate at earlier epochs.
The fact that at high redshifts the major merging rate is
much higher than at the present epoch, may be at the basis of
early spheroid formation, as well as energetic phenomena like QSOs and
submillimeter sources (see Sections 5 and
6).
CDM model,
suggesting that the model can be used to predict
the increasing merging rate at earlier epochs.
The fact that at high redshifts the major merging rate is
much higher than at the present epoch, may be at the basis of
early spheroid formation, as well as energetic phenomena like QSOs and
submillimeter sources (see Sections 5 and
6).
Using cosmological N-body simulations, we have learnt much about the clustering and properties of collapsed CDM structures. Nevertheless, important details about the innermost, less resolved regions of dark halos, where just luminous galaxies form, as well as about the angular momentum, the MAHs and their dependences on the environment, remain still unexplored. On the other hand, the potential conflicts of CDM at small scales are still open. More observational and theoretical studies are necessary to understand the depth of these conflicts.