


A model aimed to study the physics and evolution of disk galaxies should include a self-consistent and local description of dark matter processes, and gas dissipation, infall, SF, stellar evolution, and feedback. Under the assumptions of (i) dominance of accretion rather than mergers, and (ii) detailed angular momentum conservation during gas infall, several authors have been able to reproduce the main properties and correlations of disk galaxies in the hierarchical CDM scenario. The former assumption is motivated by the fact that disks are dynamically fragile objects and collisions with other galaxies heat and thicken the stellar disk beyond the level observed at present (Tóth & Ostriker 1992). The latter assumption is argueable, and is currently among the key questions of disk formation models (see e.g., van den Bosch et al. 2002). Following, we discuss the main predictions of models of disk formation inside CDM halos. A seminal paper on this subject was that of Fall & Efstathiou (1980).
The stellar surface density profile is roughly exponential, but with
an excess at the inner and outer regions
(Dalcanton et al. 1997;
Firmani & Avila-Reese
2000;
Bullock et al. 2001a;
van den Bosch 2002).
The inner cusp
may be crucial for the secular bulge formation. The surface density of the
disks depends mainly on the spin parameter
 : the angular momentum
drives the sequence from high surface brightness (HSB) to low surface
brightness (LSB) galaxies. The surface density also depends on
fgal. Mainly due to
the inside-out formation, the disks have negative color index and
metallicity gradients in agreement with observations
(Avila Reese & Firmani
2000;
Boissier & Prantzos
1999,
2001).
: the angular momentum
drives the sequence from high surface brightness (HSB) to low surface
brightness (LSB) galaxies. The surface density also depends on
fgal. Mainly due to
the inside-out formation, the disks have negative color index and
metallicity gradients in agreement with observations
(Avila Reese & Firmani
2000;
Boissier & Prantzos
1999,
2001).
The rotation curves are roughly flat. The shape of rotation curves depends on the disk surface density (Mo, Mao & White 1998; Firmani & Avila-Reese 2000). LSB galaxy models are dominated by the dark halo and even for the extreme HSB models, the CDM halo is competitive with the disk at the maximum rotation velocity. For the inner region of normal HSB galaxy rotation curves to be dominated by disk (maximum disk case), a soft core in the CDM halo is necessary (Avila-Reese et al. 2002; see also Salucci & Burkert 2000; Salucci 2001).
The slope of the infrared Tully-Fisher relation (TFR) is interpreted
as a consequence of the mass-velocity relation of the CDM halos,
determined in turn by the power spectrum of fluctuations (e.g.,
Mo et al. 1998;
Avila-Reese et al. 1998,
1999;
Steinmetz & Navarro
1999;
Firmani & Avila-Reese
2000;
Buchalter et al. 2001).
The slope of the halo mass-velocity relation derived from theory is
 3.2 - 3.4, which agrees
with the TFR slope in the infrared bands found by most observers (e.g.,
Gavazzi 1993;
Giovanelli et al. 1997;
Tully et al. 1998;
Tully & Pierce
2000).
After the formation of the disk and the stars
within it, the zero point of the model TFR is slightly fainter than
observations for the concordance
3.2 - 3.4, which agrees
with the TFR slope in the infrared bands found by most observers (e.g.,
Gavazzi 1993;
Giovanelli et al. 1997;
Tully et al. 1998;
Tully & Pierce
2000).
After the formation of the disk and the stars
within it, the zero point of the model TFR is slightly fainter than
observations for the concordance
 CDM cosmology (see
Fig. 2), and is far too faint for the SCDM one.
The introduction of soft halo cores improves the comparison with
observations
(Firmani &
Avila-Reese 2000;
Mo & Mao 2001).
The N-body+hydrodynamical simulations predict a too faint zero point even
for the
CDM cosmology (see
Fig. 2), and is far too faint for the SCDM one.
The introduction of soft halo cores improves the comparison with
observations
(Firmani &
Avila-Reese 2000;
Mo & Mao 2001).
The N-body+hydrodynamical simulations predict a too faint zero point even
for the  CDM model
(e.g.,
Steinmetz & Navarro 2000),
but this is mainly because the disks in these simulations are formed
highly concentrated
(angular momentum catastrophe), implying very peaked rotation curves.
CDM model
(e.g.,
Steinmetz & Navarro 2000),
but this is mainly because the disks in these simulations are formed
highly concentrated
(angular momentum catastrophe), implying very peaked rotation curves.
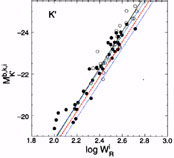 |
Figure 2. Tully-Fisher relation in the band
K as inferred by
Tully et al. (1998).
Solid line is the linear regression to
the data. Dashed line is the TFR from models of galaxy evolution
in the |
Variations in fgal and
 do not affect
significantly the TFR.
For a larger fgal, the luminosity will be higher, but
Vmax also results larger. A smaller
do not affect
significantly the TFR.
For a larger fgal, the luminosity will be higher, but
Vmax also results larger. A smaller
 implies a more
dominant disk component and therefore a larger Vmax for a
given mass; however,
the SF efficiency is higher in such a way that the stellar
mass (luminosity) for a fixed baryonic mass will be also larger
(Firmani &
Avila-Reese 2000).
This is the way we interpret why the TFRs of
LSB and HSB galaxies are similar and why the residuals of the TFR do not
correlate with the residuals of the magnitude-radius relation
(Courteau & Rix
1999).
We also find that the main source of intrinsic scatter in the TFR derives
from the scatter in the halo concentrations due to the stochastic nature
of the MAHs
(Eiseinstein & Loeb
1996);
the average scatter we measure is ~ 0.3 mag, close to the observational
estimates.
implies a more
dominant disk component and therefore a larger Vmax for a
given mass; however,
the SF efficiency is higher in such a way that the stellar
mass (luminosity) for a fixed baryonic mass will be also larger
(Firmani &
Avila-Reese 2000).
This is the way we interpret why the TFRs of
LSB and HSB galaxies are similar and why the residuals of the TFR do not
correlate with the residuals of the magnitude-radius relation
(Courteau & Rix
1999).
We also find that the main source of intrinsic scatter in the TFR derives
from the scatter in the halo concentrations due to the stochastic nature
of the MAHs
(Eiseinstein & Loeb
1996);
the average scatter we measure is ~ 0.3 mag, close to the observational
estimates.
If bulges are modeled as the gravitationally unstable stellar disk region (secular scenario), then higher surface brightness galaxies have larger bulge-to-disk ratios (van den Bosch 1998; Avila-Reese & Firmani 2000). The models reproduce the main correlations along the disk HS: the higher the SB and the redder the disk, the larger the bulge-to-disk ratio and the lower the disk gas fraction. Bulges formed secularly seem to be in agreement with observations, at least for late-type galaxies (see for a review Wyse et al. 1997).
Models can be tested even in the solar neighborhood. For a MW fiducial model (based on the statistically most probable cosmological MAH), the predicted evolution of the SF rate in the solar neighborhood agrees within the uncertainty with the evolution derived from the HR diagram provided by the Hipparco satellite (Hernández, Avila-Reese & Firmani 2001). On the other hand, chemical and photometric models, starting from the observed distributions in the MW, infer infall, structural and SF conditions similar to those expected from the hierarchical scenario (e.g., Boissier & Prantzos 1999; Prantzos, this volume). However, the inner dynamics again reveals a conflict: the CDM halo concentrates too much mass in the central regions in such a way that the shapes of the model and observed MW rotation curves do not agree. A soft core of size as inferred from observations of LSB and dwarf galaxies, eliminates the discrepancy.