3.4. Magnetic fields in the Milky Way

Since the early seventies [12, 39] the magnetic field of the Milky way (MW) was shown to be parallel to the galactic plane. RM derived from pulsars allow consistent determinations of the magnetic field direction and intensity [40, 41]. In the Milky Way, the uniform component of the magnetic field is in the plane of the galactic disk and it is thought to be directed approximately along the spiral arm. There is, though, a slight difference between the northern and southern hemisphere. While in the southern hemisphere the magnetic field is roughly 2µG, the magnetic field in the northern hemisphere is three times smaller than the one of the southern hemisphere. The magnetic field of the MW is predominantly toroidal ⁽⁹⁾. However, looking at the center of the galaxy, a poloidal component (typically 1/3 of the toroidal one) has been detected. In fact, in the central 100 pc of the MW there are in fact pooloidal (dipole) fields whose origin is probably primordial [42] (see also [43, 44]). The reason for this statement is that through the usual plasma physics mechanisms (like the dynamo theory to be discussed later in Section 4) it is hard to account for a sizable poloidal component, even if localized in the central region of the MW.

The common practice is to classify large-scale magnetic fields in spiral galaxies according to the parity of the toroidal field under reflections of the azimuthal angle [21, 14]. According to some authors this distinction palys a crucial rôle in order to assess the primordial (or non-primordial ) nature of the observed field (see, for instance, [15, 18]). In short, the virtues and limitations of the previous distinction can be summarized as follows. Suppose to plot the toroidal component of the measured magnetic field (for instance of the MW) as a function of the azimuthal angle . This is, in fact, equivalent, to plot the RM() for instance near the equatorial plane of the galaxy. Then two qualitatively different situations can arise. In the first case RM() upon rotation of around the galactic center is even and this corresponds to axisymmetric spiral galaxies (ASS). In the second case RM() upon rotation of around the galactic center is odd and this corresponds to bisymmetric spiral galaxies (BSS). This sharp distinction is invalidated by two experimental facts. First of all there may be extra phases so that it is not clear, in practice, if RM() is, predominantly, even or odd. In spite of possible ambiguities (which are, however, an experimental problem) the distinction may be very useful: if the magnetic fields would originate through some dynamo amplification the preferred configuration will be of the ASS-type and not of the BSS-type. There are strong indications that the MW is a BSS spiral [30, 31]. A related issue is the reversal of the magnetic field from one spiral arm to the other. In [31] 63 rotation measures from polarization observations of southern pulsars have been reported. For the galactic disk, convincing evidence of field reversal near the Perseus arm is presented. In the solar circle three reversals are observed: near the Carina-Sagittarius arm, near the Crux-Scutum arm, and possibly a third one in the Norma arm. These reversals are claimed to be consistent with BSS models.

Since this is a relevant point, the possible controversies arising in the analysis of the magnetic field of the MW will now be swiftly mentioned. It is appropriate, for this purpose, to give a geometrical characterization of the arm structure of the MW [45]. The spiral structure of the galaxy can be described in terms of a two-dimensional coordinate system (x, y) whose origin (0, 0) is at the galactic center. In this coordinate system the sun is located at (0, 8) where the coordinates are expressed in kpc. For each spiral arm the equation reduces to four curves, each rotated by /2 of the form:

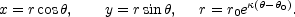(3.11)

In Eq. (3.11) r₀ ~ 2.3 kpc, ₀ ~ 0, - /2, - , -3/2, ~ 0.21. In Fig. 3 the map of the spiral arms is illustrated according to the model of Eq. (3.11). Fig. 3 is adapted from the recent paper of Vallée [45].

Figure 3. The map of the MW is illustrated. Following [45] the origin of the two-dimensional coordinate system are in the Galactic center. The two large arrows indicate one of the possible (3 or 5) field reversals observed so far. The field reversal indicated in this figure is the less controversial one.

The region with dashed lines is poorly known from the observational point of view ("zona galactica incognita" in the terminology of Vallée [45]). In terms of Fig. 3 the basic question related to the magnetic field structure concerns the relative orientation of the magnetic field direction between one arm and the nearest one. As mentioned above [30, 31] some studies suggest that three reversals are present. Some other studies [45] based on a statistical re-analysis of the most recent data from 1995 to 2001 suggest that only one reversal is observed. The two large arrows in Fig. 3 represent the field directions in the Carina-Sagittarius and in the Perseus arms. In [45] it has been argued that the magnetic field of the MW has the structure of axisymmetric spiral. However, the presence of one field reversal seems to be not fully consistent with this interpretation.

Recently [46] Han, Manchester, Lyne and Qiao, using the Parkes multibeam pulsar survey, provided further observational support for the detection of a counterclockwise magnetic field in the Norma spiral arm. The morphological properties of the magnetic field in the Carina-Sagittarius and in the Crux-Scutum arms have been confirmed [46]. These results were obtained from the analysis of pulsar rotation measures.

If the magnetic field of the MW flips its direction from one spiral arm to the other, then, as pointed out by Sofue and Fujimoto [47] the galactic magnetic field should probably be associated with a BSS model. In the Sofue-Fujimoto model the radial and azimuthal components of the magnetic field in a bisymmetric logarithmic spiral configuration is given through

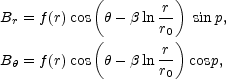(3.12)

where r₀ ~ 10.5 kpc is the galactocentric distance of the maximum of the field in our spiral arm, = 1 / tanp and p is the pitch angle of the spiral. The smooth profile f (r) can be chosen in different ways. A motivated choice is [48, 49] (see also [47])

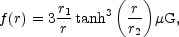(3.13)

where r₁ = 8.5 kpc is the distance of the Sun to the galactic center and r₂ = 2 kpc. The original model of SF does not have dependence in the z direction, however, the z dependence can be included and also more complicated models can be built [47]. Typically, along the z axis, magnetic fields are exponentially suppressed as exp[-z / z₀] with z₀ ~ 4 kpc.

In the BSS model there are then three issues to be determined in order to specify the parameters [50]:

• the number and location of field reversals;
• the value of the pitch angle p introduced in Eq. (3.12);
• the field strength in the disk.

The answers to these three questions are, in short, the following:

• 3 to 5 field reversals have been claimed;
• the pitch angle is determined to be p = - 8.2⁰ ± 0.5⁰ [31, 50];
• the strength of the regular field is, as anticipated 1.8 ± 0.3 µ G.

It is interesting to notice that the total field strength, in the notation of Eq. (3.1) can reach even 6 µ G indicating, possibly, a strong stochastic component. Differently from other spirals, the Milky Way has also a large radio halo. The radio-halo indicates the large-scale height of the magnetic field and its origin is unclear As far as the stochastic component of the galactic magnetic field is concerned, the situation seems to be, according to the reported results, still unclear [51, 52, 53]. It is, at present, not fully understood if the stochastic component of the galactic magnetic field is much smaller than (or of the same order of) the related homogeneous part as implied by the estimates of the total field strength.

The structure of magnetic fields can be relevant when investigating the propagation of high-energy protons [54, 55] as noticed already long ago [56]. This aspect leads to crucial (and structural) ambiguities in the analysis of the propagation of charged particles of ultra-high energy.

The current observations of ultrahigh energy cosmic rays (UHECR) do not lead to a firm evidence of the existence of a cutoff of the cosmic ray spectrum between 10¹⁹ and 10²⁰ eV. This is the celebrated Greisen, Zatsepin, Kuzmin (GZK) cutoff [57, 58]. If the source distribution of UHECR is isotropic and homogeneous because photoproduction interactions on the microwave background, then the GZK cutoff should be present. The isotropization of UHECR can be explained by scattering in large magnetic fields. This suggestion can be achieved in the presence of a sizable galactic halo. Magnetic fields may change not only the local intensity of UHECR but also their energy spectrum [59]. Various papers analyzed the acceleration and propagation of UHECR in magnetized structures (see, for instance, [60, 61, 62] and references therein).

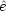
⁹ Recall that the toroidal field is defined as the vector sum of the radial and azimuthal components, i.e. _toroidal = B + B_{r r}. Back.