8.2. Faraday rotation of CMB

Large scale magnetic fields present at the decoupling epoch can also depolarize CMB [313]. The polarization of the CMB represents a very interesting observable which has been extensively investigated in the past both from the theoretical [314] and experimental points of view [315, 316]. Forthcoming satellite missions like PLANCK [317] seem to be able to achieve a level of sensitivity which will enrich decisively our experimental knowledge of the CMB polarization with new direct measurements.

If the background geometry of the universe is homogeneous but not isotropic the CMB is naturally polarized [314]. This phenomenon occurs, for example, in Bianchi-type I models [318]. On the other hand if the background geometry is homogeneous and isotropic (like in the Friedmann-Robertson-Walker case) it seems very reasonable that the CMB acquires a small degree of linear polarization provided the radiation field has a non-vanishing quadrupole component at the moment of last scattering [319, 320].

Before decoupling photons, baryons and electrons form a unique fluid which possesses only monopole and dipole moments, but not quadrupole. Needless to say, in a homogeneous and isotropic model of FRW type a possible source of linear polarization for the CMB becomes efficient only at the decoupling and therefore a small degree of linear polarization seems a firmly established theoretical option which will be (hopefully) subjected to direct tests in the near future. The linear polarization of the CMB is a very promising laboratory in order to directly probe the speculated existence of a large scale magnetic field (coherent over the horizon size at the decoupling) which might actually rotate (through the Faraday effect) the polarization plane of the CMB.

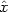Consider, for instance, a linearly polarized electromagnetic wave of physical frequency travelling along the direction in a plasma of ions and electrons together with a magnetic field () oriented along an arbitrary direction ( which might coincide with 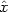in the simplest case). If we let the polarization vector at the origin (x = y = z = 0, t = 0) be directed along the 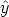axis, after the wave has traveled a length x, the corresponding angular shift ( ) in the polarization plane will be :

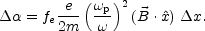(8.30)

From Eq. (8.30) by stochastically averaging over all the possible orientations of and by assuming that the last scattering surface is infinitely thin (i.e. that xf_e n_{e T}^-1 where _T is the Thompson cross section) we get an expression connecting the RMS of the rotation angle to the magnitude of 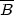at t t_dec

(8.31)

(in the previous equation we implicitly assumed that the frequency of the incident electro-magnetic radiation is centered around the maximum of the CMB). We can easily argue from Eq. (8.31) that if B(t_dec) B_c the expected rotation in the polarization plane of the CMB is non negligible. Even if we are not interested, at this level, in a precise estimate of , we point out that more refined determinations of the expected Faraday rotation signal (for an incident frequency _M ~ 30 GHz) were recently carried out [321, 322] leading to a result fairly consistent with (8.30).

Then, the statement is the following. If the CMB is linearly polarized and if a large scale magnetic field is present at the decoupling epoch, then the polarization plane of the CMB can be rotated [313]. The predictions of different models can then be confronted with the requirements coming from a possible detection of depolarization of the CMB [313].