Up to now large scale magnetic fields have been treated in different frameworks but always within a perturbative approach. However, magnetic fields can also break explicitely the isotropy (but not the homogeneity) of the background geometry.
Suppose that at some time t1 the Universe becomes transparent to radiation and suppose that, at the same time, the four-dimensional background geometry (which we assume, for simplicity, spatially flat) has a very tiny amount of anisotropy in the scale factors associated with different spatial directions, namely
 |
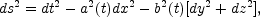(9.1) |
where b(t), as it will be clear in a moment, has to be only slightly different from a(t). The electromagnetic radiation propagating along the x and y axes will have a different temperature, namely
 |
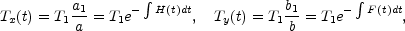(9.2) |
where H(t) and F(t) are the two Hubble factors associated, respectively with a(t) and b(t). The temperature anisotropy associated with the electromagnetic radiation propagating along two directions with different expansion rates can be roughly estimated, in the limit H(t) - F(t) << 1, as
 |
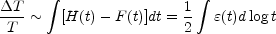(9.3) |
where, in the second equality, we assumed that the deviations from the
radiation dominated expansion can be written as
F(t) ~ (1 -
(t)) /
2t with
|(t)|
<< 1. The function
can be connected
with the shear parameter, i.e.
[H(t) - F(t)] / [H(t) +
2F(t)] which
measures the anisotropy in the expansion. In the standard context
[284,
285]
Einstein equations are solved in the metric (9.1) with fluid sources and
in the presence of a magnetic field. The shear parameter is then
connected with the magnetic field intensity.
The dynamical origin of the primordial anisotropy in the expansion can be connected with the existence of a primordial magnetic field (not dynamically generated but postulated as an initial condition) or with some other sources of anisotropic pressure and, therefore, the possible bounds on the temperature anisotropy can be translated into bounds on the time evolution of the anisotropic scale factors [303].
Today the amount of anisotropy in the expansion must be very small because of the effect we just described. In the present Section some highly speculative considerations on the possible rôle of magnetic fields in the early Universe will be intrtoduced. In spite of the fact that magnetic fields must be sufficiently small today, in the past history of the Universe they might have been very large even modifying the dynamics of the geometry. During the magnetic phase the anisotropy in the expansion will be constant (or even grow). However, after the magnetic phase a sufficienly long radiation dominated phase may isotropize the background leading to a tiny amount of anisotropy in the expansion. This is the basic scenario invoked long ago by Zeldovich [284, 285].
In modern approaches to cosmology, the dynamics of the Universe at very high densities is often discussed in terms of the low-energy string effective action. It is then useful to analyze the Zeldovich proposal in terms of the modern perspective.
In the low energy limit, the dilaton field is directly coupled to the kinetic term of the Maxwell field [332]
 |
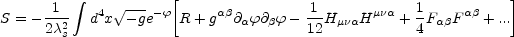(9.4) |
where F
=
[
A] is the Maxwell field strength and
µ is the
covariant derivative with respect to the String frame metric
gµ
.
Notice that
Hµ is the antisymmetric
field strength. In Eq. (9.4)
the ellipses stand for a possible (non-perturbative) dilaton potential
and for the string tension corrections parameterized by
' =
s2.
In Eq. (9.4)
Fµ can
be thought as the Maxwell field associated with a U(1) subgroup of
E8 × E8.
Consider a spatially flat background configuration with vanishing
antysimmetric field strangth
(Hµ = 0) and vanishing
dilaton potential.
The dilaton depends only on time and the metric will be taken fully
anisotropic since we want to study possible solutions with a homogeneous
magnetic field which is expected to break the isotropy of the background:
 |
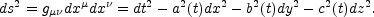(9.5) |
By varying the effective action with respect to
,
gµ and the
vector potential Aµ we get, respectively
 |
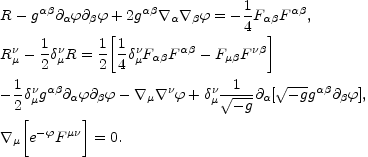(9.6)
|
where µ
denotes covariant differentiation with respect
to the metric of Eq. (9.5). Inserting Eq. (5.58) into Eq. (9.7) we
get that Eq. (9.7) can be expressed as
 |
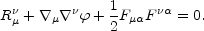(9.9) |
Consider now a homogeneous magnetic field directed along the x axis. The generalized Maxwell equations (9.8) and the associated Bianchi identities can then be trivially solved by the field strength Fyz = - Fzy. The resulting system of equations (5.58), (9.9) can than be written, in the metric of Eq. (9.5), as
 |
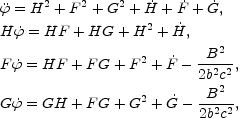(9.10) (9.11) (9.12) (9.13) |
where Eqs. (9.10)-(9.13) correspond, respectively to the (00) and (ii) components of Eq. (9.9).
The solution of Eqs. (9.10)-(9.13)
 |
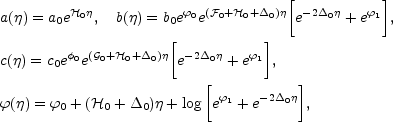(9.14) (9.15) |
where
 |
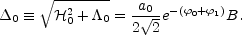(9.16) |
The solution given in Eq. (9.16) s given in terms of a new variable (a generalized conformal time) defined by the following differential relation
 |
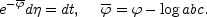(9.17) |
These solutions represent the generalization of pre-big bang solutions [123] to the case where a constant magnetic field is included. Generalizations of the solution (9.16) can be obtained in various models anisotropic (but homogeneous) models of the Bianchi class [337] like Bianchi I, II, III, VI-1 and VII0 according to the usual classification which can be found, for instance, in [333]. Further generalizations of the solution (9.16) are possible in the Kantowski-Sachs metric with a magnetic field aligned alond the radial coordinate [335, 336].
Magnetized cosmological solutions can be used in order to describe some early phase in the life of the universe. This highly speculative idea may be implemented in semi-realistic models provided the large anisotropy in the expansion decays at later epochs. In the standard context [284, 285] the only source of isotropization is the evolution in a radiation dominated background since the shear parameter decays if the background is dominated by radiation. If quadratic corrections are present, an initially anisotropic solution becomes isotropic as a consequence of the dynamical properties of the evolution equations as discussed in detail in [332].
Gauge fields have also been studied as a source of inflationary evolution by Ford [338] and later by Lidsey [339, 340]. The gauge kinetic term is supplemented by a potential which is a function of Aµ Aµ. Both exponential inflation [338] and power-law inflation [339] can be realized in these models.