


Two fluids and one-fluid MHD equations
In a two-fluid plasma description the charge carriers are the ions (for simplicity we can think of them as protons) and the electrons. The two fluid equations treat the ions and the electrons as two conducting fluids which are coupled as in Eqs. (4.8)-(4.12). Given the two- fluid description, one-fluid variables can be defined directly in terms of the two-fluid variables
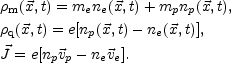 |
(A.1) |
In the case of a globally neutral plasma
ne ~ np = nq and
 q =
0. The ion and electron equations then become
q =
0. The ion and electron equations then become
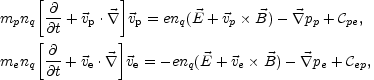 |
(A.2) (A.3) |
where  pe and
pe and
 pe are the
collision terms. In the globally neutral case the center of mass velocity
becomes
pe are the
collision terms. In the globally neutral case the center of mass velocity
becomes
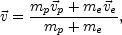 |
(A.4) |
and the one-fluid mass and charge density conservations become
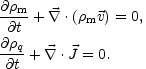 |
(A.5) (A.6) |
Summing up Eqs. (A.2) and (A.3) leads, with some algebra involving the continuity equation, to the momentum transport equation in the one-fluid theory:
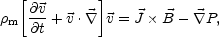 |
(A.7) |
where P = Pe + Pi.
In Eq. (A.7) the collision term vanishes if there are no neutral
particles, i.e. if the plasma is fully ionized.
The final equation of the one-fluid description is obtained by taking
the difference of Eqs. (A.2) and (A.3)
after having multiplied Eq. (A.2) by me and Eq. (A.3)
by mp. This procedure is more tricky and it is
discussed in standard textbooks of plasma physics
[85,
86].
The key points in the derivation are that the limit for
me / mp
 0 must be taken. The
problem with this procedure is that the subtraction of the two
mentioned equations does not guarantee that viscous and collisional
effects are negligible.
The result of this procedure is the so-called one-fluid generalized Ohm law:
0 must be taken. The
problem with this procedure is that the subtraction of the two
mentioned equations does not guarantee that viscous and collisional
effects are negligible.
The result of this procedure is the so-called one-fluid generalized Ohm law:
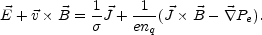 |
(A.8) |
The term
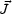 × B
is nothing but the Hall current and
× B
is nothing but the Hall current and
 Pe is often called thermoelectric term. Finally the term
Pe is often called thermoelectric term. Finally the term
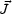 /
/
 is the resistivity term
and
is the resistivity term
and  is
the conductivity of the one-fluid description. In Eq. (A.8) the
pressure has been taken to be isotropic.
This is, however, not a direct consequence of the calculation presented
in this Appendix but it is an assumption
which may (and should) be relaxed in some cases. In the plasma physics
literature
[85,
86]
the anisotropic pressure contribution is neglected for the simple reason
that experiments terrestrial plasmas show that this terms is often
negligible.
is
the conductivity of the one-fluid description. In Eq. (A.8) the
pressure has been taken to be isotropic.
This is, however, not a direct consequence of the calculation presented
in this Appendix but it is an assumption
which may (and should) be relaxed in some cases. In the plasma physics
literature
[85,
86]
the anisotropic pressure contribution is neglected for the simple reason
that experiments terrestrial plasmas show that this terms is often
negligible.
Conservation laws in resistive MHD
Consider and arbitrary closed surface
 which moves with the
plasma. Then, by definition of the bulk velocity of the plasma
(
which moves with the
plasma. Then, by definition of the bulk velocity of the plasma
( we can also write
d
we can also write
d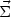 =
=
 ×
d
×
d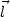 d
d . The
(total) time derivative of the flux can therefore be expressed as
. The
(total) time derivative of the flux can therefore be expressed as
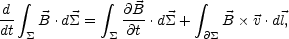 |
(A.9) |
where 
 is the boundary of
is the boundary of
 . Using now the
properties of the vector products
(i.e.
. Using now the
properties of the vector products
(i.e.  ×
×
 .
d
.
d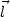 =
-
=
-  ×
×
 .
d
.
d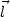 ) we can
express
) we can
express  ×
×
 though the Ohm
law given in Eq. (4.23) and we obtain that
though the Ohm
law given in Eq. (4.23) and we obtain that
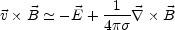 |
(A.10) |
Using now Eq. (A.9) together with the Stokes theorem, the following expression can be obtained
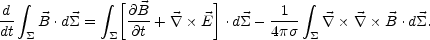 |
(A.11) |
From the Maxwell's equations the first part at the right hand side of Eq. (A.11) is zero and Eq. (4.24), expressing the Alfvén theorem, is recovered.
With similar algebraic manipulations (involving the use of various
vector identities), the conservation of the
magnetic helicity can be displayed. Consider a closed volume in the plasma,
then we can write that
dV = d3 x =

 .
d
.
d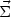 d
d

 .
.

 d
d d
d where
where
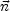 is the unit
vector normal to
is the unit
vector normal to  (the boundary of V, i.e.
(the boundary of V, i.e.
 =
=
 V) and
V) and

 is the component of the
bulk velocity orthogonal to
is the component of the
bulk velocity orthogonal to
 V. The
(total) time derivative of the magnetic helicity can now be written as
V. The
(total) time derivative of the magnetic helicity can now be written as
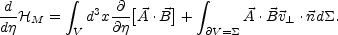 |
(A.12) |
The partial derivative at the right hand side of Eq. (A.12) can be made explicit. Then the one-fluid MHD equations should be used recalling that the relation between the electromagnetic fields and the vector potential, for instance in the Coulomb gauge. Finally using again the Ohm law and transforming the obtained surface integrals into volume integrals (through the divergence theorem) Eq. (4.27), expressing the conservation of the helicity, can be obtained.
In spite of the fact that the conservation of the magnetic helicity can be derived in a specific gauge, the magnetic helicity is indeed a gauge invariant quantity. Consider a gauge transformation
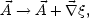 |
(A.13) |
then the magnetic helicity changes as
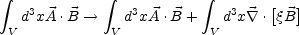 |
(A.14) |
(in the second term at the right hand side we used the fact that the magnetic field is divergence free). By now using the divergence theorem we can express the volume integral as
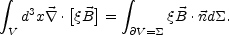 |
(A.15) |
Now if, as we required,
 .
.
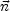 = 0 in
= 0 in
 V, the
integral is exactly zero and
V, the
integral is exactly zero and
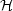 M is gauge
invariant. The condition
M is gauge
invariant. The condition
 .
.
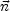 = 0 is not
specific of a particular profile of the magnetic field. It can be always
achieved by slicing the volume of integration in
small flux tubes where, by definition, the magnetic field
is orthogonal to the walls of the flux tube.
= 0 is not
specific of a particular profile of the magnetic field. It can be always
achieved by slicing the volume of integration in
small flux tubes where, by definition, the magnetic field
is orthogonal to the walls of the flux tube.