4. GALAXY COLLISIONS

If the dark halos of galaxies in rich clusters are as large as the preceding discussion suggests, then a typical bright galaxy will undergo a number of interpenetrating collisions with other galaxies over a Hubble time. Because galaxy orbital velocities in clusters are usually much greater than their internal velocities, few if any of these encounters will result in mergers. (This may not be true for galaxies whose orbits confine them to the cluster core, especially if a supermassive "cD" galaxy is present; see the next section.) However close collisions might be effective at removing dark matter from galactic halos. One of the first discussions of collisional stripping in the context of galaxy clusters was that of Richstone (1976), who estimated that, if all of a cluster's dark matter was originally bound to the galaxies in the form of massive halos, all but ~ 10% would be liberated in a Hubble time. Richstone's calculation ignored tidal forces due to the cluster mean field; as we have seen, tidal truncation by itself guarantees that roughly the same fraction of the dark matter will be smoothly distributed once a cluster has reach equilibrium, even in the absence of collisions. Nevertheless we cannot quite rule out collisions as unimportant in clusters, because Richstone's (1976) study (as well as most later studies) was based on rather crude estimates of the collisional mass loss rate. Furthermore, an occasional close collision between two massive galaxies could substantially affect their observable properties, even if typical collisions are relatively "mild".

Consider a gravitational encounter between two galaxies. During the encounter, each star in the "test" galaxy feels a tidal acceleration toward the "perturber" of order

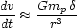(17)

where and r are the separations of the star from the center of the test galaxy and the perturber, respectively, and m_p is the mass of the perturber. Since encounters in clusters typically occur at high speeds, we can ignore to first order the orbital motion of the star within the test galaxy when computing the total momentum given to it by the perturber (the "impulse approximation"). Thus

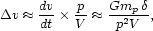(18)

where p is the collision impact parameter and V is the encounter velocity. Equation (18) implies that close, slow encounters are the most effective at removing mass. Notice however that this equation can only be valid over a limited range of impact parameters. For p >> , the collision is slow, and the impulse approximation does not apply. For p , the galaxies are close or interpenetrating, and the tidal acceleration will not be given by the simple formula (17). Furthermore, the fraction of the test galaxy's mass that acquires positive binding energy and escapes must depend strongly on its internal velocity distribution. Thus an accurate estimate of the mass loss resulting from an encounter requires a full N-body simulation.

The most detailed study to date of this problem is that of Aguilar and White (1985), who simulated a large number of collisions between spherical galaxies with either of two density profiles. They found that close collisions, which are the only important ones for mass loss, are not well described by the tidal approximation; in particular, the fractional mass loss does not depend on simple powers of the encounter parameters as equation (18) suggests and as most previous workers (e.g. Richstone 1976, Merritt 1984a) have assumed. In order to estimate how greatly those earlier studies were in error, Aguilar and White (1985) calculated the mean rate at which a galaxy would lose mass due to encounters with a uniform background of equal-mass galaxies with a Maxwellian distribution of velocities. They found:

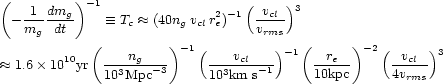(19)

where n_g is the number density of galaxies, r_e is the galaxy "effective" (projected half-mass) radius, and v_rms and v_cl are the galaxy internal and orbital velocity dispersions, respectively. Perhaps fortuitously, equation (19) agrees rather well with Richstone's (1976) estimate when v_cl / v_rms 4, appropriate for the rich-cluster environment which Richstone considered. In these clusters, collisions would not be expected to liberate much mass in a Hubble time unless galaxies managed to retain halos much more extensive than those permitted by the mean tidal field. However the strong dependence of T_c on v_cl suggests that collisions might be very effective in poorer clusters, for which v_cl 2v_rms.

It has occasionally been suggested (e.g. Gallagher and Ostriker 1972) that close collisions between galaxies in dense cluster environments might liberate a substantial amount of luminous material over a Hubble time, thus contributing to the luminosity of a central cD galaxy. The simulations of Aguilar and White (1985) suggest that this is very unlikely to be an important process unless a substantial fraction of a typical galaxy's light lies more than ~ 10 kpc from its center. On the other hand, if a supermassive galaxy should happen to be present ab initio at the center of a rich cluster, then a modification of the arguments in the preceding section suggest that it might be responsible for tidally removing at least a moderate amount of light from other galaxies. If the mass of the central galaxy is distributed like an isothermal sphere, then its mass within a radius r is m_cD 2_cD² r / G, and its average density is <> _cD² / 2Gr². The tidal truncation calculations described above then give for the limiting mass of a galaxy that passes within this radius:

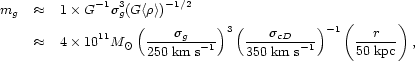(20)

and for its limiting radius,

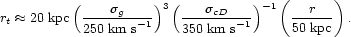(21)

Thus a bright galaxy whose pericenter lay within ~ 30 kpc of the central cD would probably lose a significant fraction of its luminous matter after a few orbits; the mass of a cD galaxy that extends to this radius would be 2 × 10¹² M, which is not unreasonable. Whether this mechanism is capable of liberating enough luminous matter in a Hubble time to produce a "cD envelope", with a total luminosity ~ 5L^*, is questionable, however.