


6.1. History and general aspects of bias
In order to make full use of the cosmological information encoded in large-scale structure, it is essential to understand the relation between the number density of galaxies and the mass density field. It was first appreciated during the 1980s that these two fields need not be strictly proportional. Until this time, the general assumption was that galaxies `trace the mass'. Since the mass density is a continuous field and galaxies are point events, the approach is to postulate a Poisson clustering hypothesis, in which the number of galaxies in a given volume is a Poisson sampling from a fictitious number-density field that is proportional to the mass. Thus within a volume V,
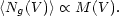 |
(96) |
With allowance for this discrete sampling, the observed numbers of galaxies, Ng, would give an unbiased estimate of the mass in a given region.
The first motivation for considering that galaxies might in fact be biased
mass tracers came from attempts to reconcile the
 m = 1
Einstein-de Sitter model with observations. Although M / L
ratios in rich clusters argued for dark matter, as first shown by
Zwicky (1933),
typical blue values of
M / L
m = 1
Einstein-de Sitter model with observations. Although M / L
ratios in rich clusters argued for dark matter, as first shown by
Zwicky (1933),
typical blue values of
M / L  300h implied only
300h implied only
 m
m
 0.2 if
they were taken to be universal. Those who argued that the value
0.2 if
they were taken to be universal. Those who argued that the value
 m = 1 was
more natural (a greatly increased camp after the advent of inflation)
were therefore forced to postulate that the efficiency of galaxy
formation was enhanced in dense environments: biased galaxy formation.
m = 1 was
more natural (a greatly increased camp after the advent of inflation)
were therefore forced to postulate that the efficiency of galaxy
formation was enhanced in dense environments: biased galaxy formation.
We can note immediately that a consequence of this bias in density will be to affect the velocity statistics of galaxies relative to dark matter. Both galaxies and dark-matter particles follow orbits in the overall gravitational potential well of a cluster; if the galaxies are to be more strongly concentrated towards the centre, they must clearly have smaller velocities than the dark matter. This is the phenomenon known as velocity bias (Carlberg, Couchman & Thomas 1990).
An argument for bias at the opposite extreme of density arose
through the discovery of large voids in the galaxy distribution
(Kirshner et al. 1981).
There was a reluctance to believe that such vast
regions could be truly devoid of matter -
although this was at a time before the discovery
of large-scale velocity fields.
This tendency was given further stimulus through the work of
Davis, Efstathiou, Frenk
& White (1985),
who were the first to calculate N-body models
of the detailed nonlinear structure arising in
CDM-dominated universes. Since the CDM spectrum
curves slowly between effective indices
of n = - 3 and n = 1, the correlation function
steepens with time. There is therefore a unique epoch when
 will have the
observed slope of -1.8. Davis et al. identified this
epoch as the present and then noted that, for
will have the
observed slope of -1.8. Davis et al. identified this
epoch as the present and then noted that, for
 m = 1, it
implied a rather low amplitude of fluctuations:
r0 = 1.3h-2 Mpc. An independent
argument for this low
amplitude came from the size of the peculiar velocities
in CDM models: if the spectrum was given an amplitude corresponding to the
m = 1, it
implied a rather low amplitude of fluctuations:
r0 = 1.3h-2 Mpc. An independent
argument for this low
amplitude came from the size of the peculiar velocities
in CDM models: if the spectrum was given an amplitude corresponding to the
 8
8
 1 seen in the galaxy
distribution, the pairwise dispersion was
1 seen in the galaxy
distribution, the pairwise dispersion was
 p
p
 1000 - 1500 km
s-1, around 3 times the observed value.
What seemed to be required was a galaxy correlation function that was an
amplified version of that for mass. This was exactly the
phenomenon analysed for Abell clusters by
Kaiser (1984),
and thus was born the idea of high-peak bias: bright
galaxies form only at the sites of high peaks in the
initial density field. This was developed in some analytical detail by
Bardeen et al. (1986),
and was implemented in the simulations of
Davis et al. (1985).
1000 - 1500 km
s-1, around 3 times the observed value.
What seemed to be required was a galaxy correlation function that was an
amplified version of that for mass. This was exactly the
phenomenon analysed for Abell clusters by
Kaiser (1984),
and thus was born the idea of high-peak bias: bright
galaxies form only at the sites of high peaks in the
initial density field. This was developed in some analytical detail by
Bardeen et al. (1986),
and was implemented in the simulations of
Davis et al. (1985).
As shown below, the high-peak model produces a linear amplification of large-wavelength modes. This is likely to be a general feature of other models for bias, so it is useful to introduce the linear bias parameter:
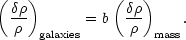 |
(97) |
This seems a reasonable assumption when

 /
/
 << 1,
although it leaves open the question of how the effective value of b
would be expected to change on nonlinear scales.
Galaxy clustering on large scales therefore allows us to determine
mass fluctuations only if we know the value of b.
When we observe large-scale galaxy clustering, we are only
measuring b2
<< 1,
although it leaves open the question of how the effective value of b
would be expected to change on nonlinear scales.
Galaxy clustering on large scales therefore allows us to determine
mass fluctuations only if we know the value of b.
When we observe large-scale galaxy clustering, we are only
measuring b2
 mass(r) or
b2
mass(r) or
b2 2mass(k).
2mass(k).
Later studies of bias concentrated on general models. A fruitful assumption is that bias is local, so that the number density of galaxies is some nonlinear function of the mass density
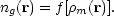 |
(98) |
Coles (1993) proved the powerful result that, whatever the function f may be, the quantity
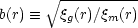 |
(99) |
had to show a monotonic dependence on scale, provided the mass density field had Gaussian statistics. An interesting concrete example of this is provided by the lognormal density field (Coles & Jones 1991); this is generated by exponentiation of a Gaussian field:
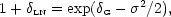 |
(100) |
where  2 is
the total variance in the Gaussian field. These authors argue that this
analytical form is a reasonable approximation
to the exact nonlinear evolution of the mass density
distribution function, preventing the unphysical values
2 is
the total variance in the Gaussian field. These authors argue that this
analytical form is a reasonable approximation
to the exact nonlinear evolution of the mass density
distribution function, preventing the unphysical values
 < - 1.
This non-Gaussian model is built upon an underlying Gaussian field,
so the joint distribution of the density
at n points is still known. This means that the
correlations are simple enough to calculate, the result being
< - 1.
This non-Gaussian model is built upon an underlying Gaussian field,
so the joint distribution of the density
at n points is still known. This means that the
correlations are simple enough to calculate, the result being
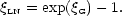 |
(101) |
This says that  on large scales is unaltered by nonlinearities
in this model; they only add extra small-scale correlations.
Using the lognormal model as a hypothetical nonlinear density
field, we can now introduce bias. A nonlinear local transformation
on large scales is unaltered by nonlinearities
in this model; they only add extra small-scale correlations.
Using the lognormal model as a hypothetical nonlinear density
field, we can now introduce bias. A nonlinear local transformation
 g
g

 LNb then gives a correlation function
1 +
LNb then gives a correlation function
1 +  g
= (1 +
g
= (1 +  LN)b2
(Mann, Peacock &
Heavens 1998).
The linear bias parameter is b, but the correlations steepen
on small scales, as expected for Coles' result.
LN)b2
(Mann, Peacock &
Heavens 1998).
The linear bias parameter is b, but the correlations steepen
on small scales, as expected for Coles' result.
In reality, bias is unlikely to be completely causal, and this has led some workers to explore stochastic bias models, in which
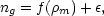 |
(102) |
where  is a random
field that is uncorrelated with the mass density
(Pen 1998;
Dekel & Lahav 1999).
This means we need to consider not only the bias parameter
defined via the ratio of correlation functions, but also
the correlation coefficient, r, between galaxies and mass:
is a random
field that is uncorrelated with the mass density
(Pen 1998;
Dekel & Lahav 1999).
This means we need to consider not only the bias parameter
defined via the ratio of correlation functions, but also
the correlation coefficient, r, between galaxies and mass:
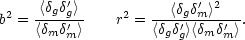 |
(103) |
Although truly stochastic effects are possible in galaxy formation, a relation of the above form is expected when the galaxy and mass densities are filtered on some scale (as they always are, in practice). Just averaging a galaxy density that is a nonlinear function of the mass will lead to some scatter when comparing with the averaged mass field; a scatter will also arise when the relation between mass and light is non-local, however, and this may be the dominant effect.