6.5. The halo model - I: mass

The formation of galaxies must be a non-local process to some extent, and the modern paradigm was introduced by White & Rees (1978): galaxies form through the cooling of baryonic material in virialized haloes of dark matter. The virial radii of these systems are in excess of 0.1 Mpc, so there is the potential for large differences in the correlation properties of galaxies and dark matter on these scales. The `halo model' addresses this by creating a density field in which dark-matter haloes are superimposed. The key feature that allows bias to be included is to encode all the complications of galaxy formation via the halo occupation number: the number of galaxies found above some luminosity threshold in a virialized halo of a given mass.

To some extent, this is a very old idea: one of the earliest suggested models for the galaxy correlation function was to consider a density field composed of randomly-placed independent clumps with some universal density profile (Neyman, Scott & Shane 1953; Peebles 1974). Since the clumps are placed at random (with number density n), the only excess neighbours to a given mass point arise from points in the same clump, and the correlation function is straightforward to compute in principle. For the case where the clumps have a power-law density profile,

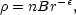(112)

truncated at r = R, the small-r behaviour of the correlation function is r^3-2, provided 3/2 < < 3. For smaller values of , (r) tends to a constant as r 0. In the isothermal = 2 case, the correlation function for r << R is

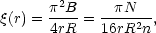(113)

where N is the total number of particles per clump (Peebles 1974).

Figure 12. A comparison of various possible density profiles for virialized haloes. The dotted line is a singular isothermal sphere. The solid lines show haloes with formation redshifts of 0 and 5 according to NFW ( = 1) and M99.

The general result is that the correlation function is less steep at small r than the clump density profile, which is inevitable because an autocorrelation function involves convolving the density field with itself. A long-standing problem for this model is therefore that the predicted correlation function is much flatter than is observed for galaxies: r^-1.8 is the canonical slope, apparently requiring clumps with very steep density profiles, = 2.4. This is not in agreement with the profiles of dark-matter haloes as `observed' in numerical simulations.

Traditionally, virialized systems have been found by a criterion based on percolation (`friends-of-friends'), such that the mean density is about 200 times the mean. Sometimes, the criterion is taken as a density of 200 times the critical value. We shall use the former definition:

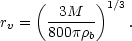(114)

Thus r_v is related to the Lagrangian radius containing the mass via r_v = R / 200^1/3. Of course, the density contrast used to define the boundary of an object is somewhat arbitrary. Fortunately, much of the mass resides at smaller radii, near a `core radius'. These core radii are relatively insensitive to the exact definition of virial radius.

The simplest model for the density structure of the virialized system is the singular isothermal sphere: = _v² / (2Gr²), or

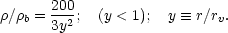(115)

A more realistic alternative is the profile proposed by Navarro, Frenk & White (1996; NFW):

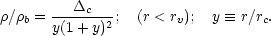(116)

The parameter _c is related to the core radius and the virial radius via

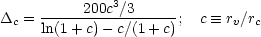(117)

(we change symbol from NFW's _c to avoid confusion with the linear-theory density threshold for collapse, and also because our definition of density is relative to the mean, rather than the critical density). NFW showed that _c is related to collapse redshift via

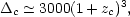(118)

An advantage of the definition of virial radius used here is that _c is independent of (for given z_c), whereas NFW's _c is .

The above equations determine the concentration, c = r_v / r_c implicitly, hence in principle giving r_c in terms of r_v once _c is known. NFW give a procedure for determining z_c. A simplified argument would suggest a typical formation era determined by D(z_c) = 1 / , where D is the linear-theory growth factor between z = z_c and the present, and is the dimensionless fluctuation amplitude corresponding to the system in units of the rms: _c / (M), where _c 1.686. For very massive systems with >> 1, only rare fluctuations have collapsed by the present, so z_c is close to zero. This suggests the interpolation formula

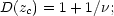(119)

The NFW formula is actually of this form, except that the 1 / term is multiplied by a spectrum-dependent coefficient of order unity. It has been claimed by Moore et al. (1999; M99) that the NFW density profile is in error at small r. M99 proposed the alternative form

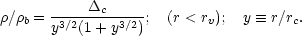(120)

It is straightforward to use this in place of the NFW profile.

We now compute the power spectrum for the halo model. Start by distributing point seeds throughout the universe with number density n, in which case the power spectrum of the resulting density field is just shot noise:

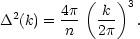(121)

Here, we use a dimensionless notation for the power spectrum: ² is the contribution to the fractional density variance per unit interval of ln k. In the convention of Peebles (1980), this is

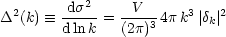(122)

(V being a normalization volume), and the relation to the correlation function is

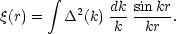(123)

The density field for a distribution of clumps is produced by convolution of the initial field of delta-functions, so the power spectrum is simply modified by the squared Fourier transform of the clump density profile:

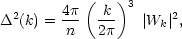(124)

where

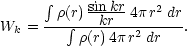(125)

For a practical calculation, we should also use the fact that hierarchical models are expected to contain a distribution of masses of clumps. If we use the notation f (M) dM to denote the number density of haloes in the mass range dM, the effective number density in the shot noise formula becomes

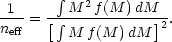(126)

The window function also depends on mass, so the overall power spectrum is

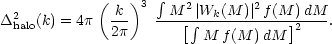(127)

The normalization term M f (M) dM just gives the total background density, _b, so there is only a single numerical integral to perform. Using this model, it is then possible to calculate the correlations of the nonlinear density field, neglecting only the large-scale correlations in halo positions. The power spectrum determined in this way is shown in figure 13, and turns out to agree very well with the exact nonlinear result on small and intermediate scales. The lesson here is that a good deal of the nonlinear correlations of the dark matter field can be understood as a distribution of random clumps, provided these are given the correct distribution of masses and mass-dependent density profiles.

Figure 13. The decomposition of the mass power spectrum according to the halo model, for the flat m = 0.3, = 0.2, 8 = 0.8 case. The dashed line shows linear theory, and the open circles show the predicted 1-halo contribution. Adding in linear theory to produce the correct large-scale clustering yields the solid points. The full lines show the contribution of different mass ranges to the 1-halo term: bins of width a factor 10 in width, starting at 1010 -1011 h-1 M and ending at 1015 -1016 h-1 M. The more massive haloes have larger virial radii and hence filter the power spectrum on progressively larger scales. The majority of the quasilinear power is contributed by the haloes near the peak in the mass function at 1014 -1015 h-1 M.

So far, we have ignored any spatial correlations in the halo positions. A simple guess for amending this is to add the linear power spectrum to the power generated by the halo structure:

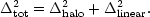(128)

The justification for this is that the extra small-scale power introduced by nonlinear evolution is associated with the internal structure of the haloes. In practice, this model works extremely well, giving an almost perfect description of the power spectrum on all scales. This is a novel way of looking at the features in the nonlinear spectrum, particularly the steep rise between k 0.5 h Mpc^-1 and k 5 h Mpc^-1, and the flattening on smaller scales. According to the ideas presented here, the flat small-scale spectrum arises because haloes have central density profiles rising as r^-1.5, but not much faster. The sharp fall in power at smaller k reflects the cutoff at the virial radii of the haloes that dominate the correlation signal.

It might be objected that this model is still not completely realistic, since we have treated haloes as smooth objects and ignored any substructure. At one time, it was generally believed that collisionless evolution would lead to the destruction of galaxy-scale haloes when they are absorbed into the creation of a larger-scale nonlinear system such as a group or cluster. However, it turns out that this `overmerging problem' was only an artefact of inadequate resolution (see e.g. van Kampen 2000). When a simulation is carried out with ~ 10⁶ particles in a rich cluster, the cores of galaxy-scale haloes can still be identified after many crossing times (Ghigna et al. 1998). This substructure must have some effect on the correlations of the density field, and indeed Valageas (1999) has argued that the high-order correlations of the density field seen in N-body simulations are inconsistent with a model where the density file is composed of smooth virialized haloes. Nevertheless, substructure seems to be unimportant at the level of two-point correlations.

The existence of substructure is important for the obvious next step of this work, which is to try to understand galaxy correlations within the current framework. It is clear that the galaxy-scale substructure in large dark-matter haloes defines directly where luminous galaxies will be found, giving hope that the main features of galaxy formation can be understood principally in terms of the dark-matter distribution. Indeed, if catalogues of these `sub-haloes' are created within a cosmological-sized simulation, their correlation function is known to differ from that of the mass (e.g. Klypin et al. 1999; Ma 1999). The model of a density field consisting of smooth haloes may therefore be a useful description of the galaxy field, and this is explored in the following section.