


8.2. Horizon-angle degeneracy
As we have seen, the geometrical degeneracy can be broken either by
additional information (such as a limit on h), or by invoking
a theoretical prejudice in favour of flatness. Even
for flat models, however, there still exists a version of the same
degeneracy. What determines the CMB peak locations for flat models?
The horizon size at last scattering is
DHLS = 184
( m
h2)-1/2 Mpc. The angular scale of these peaks
depends on the ratio between the horizon size at last scattering
and the present-day horizon size for flat models:
m
h2)-1/2 Mpc. The angular scale of these peaks
depends on the ratio between the horizon size at last scattering
and the present-day horizon size for flat models:
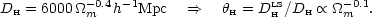 |
(152) |
(using the approximation of
Vittorio & Silk
1985).
This yields an angle scaling as
 m-0.1, so that the
scale of the acoustic peaks is apparently almost independent
of the main parameters.
m-0.1, so that the
scale of the acoustic peaks is apparently almost independent
of the main parameters.
However, this argument is incomplete because the earlier expression for DH(zLS) assumes that the universe is completely matter dominated at last scattering, and this is not perfectly true. The comoving sound horizon size at last scattering is defined by (e.g. Hu & Sugiyama 1995)
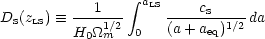 |
(153) |
where vacuum energy is neglected at these high redshifts;
the expansion factor
a  (1 +
z)-1 and
aLS, aeq are the values at last
scattering and matter-radiation equality respectively.
In practice, zLS
(1 +
z)-1 and
aLS, aeq are the values at last
scattering and matter-radiation equality respectively.
In practice, zLS
 1100 independent of the
matter and baryon densities, and
cS is fixed by
1100 independent of the
matter and baryon densities, and
cS is fixed by
 b. Thus
the main effect is that aeq depends
on
b. Thus
the main effect is that aeq depends
on  m.
Dividing by DH(z = 0) therefore
gives the angle subtended today by the light horizon as
m.
Dividing by DH(z = 0) therefore
gives the angle subtended today by the light horizon as
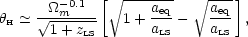 |
(154) |
where zLS = 1100 and aeq = (23900
 m)-1.
This remarkably simple result captures most
of the parameter dependence of CMB peak locations within
flat
m)-1.
This remarkably simple result captures most
of the parameter dependence of CMB peak locations within
flat  CDM models.
Differentiating this equation near a fiducial
CDM models.
Differentiating this equation near a fiducial
 m = 0.147 gives
m = 0.147 gives
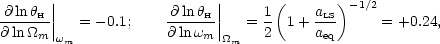 |
(155) |
in good agreement with the numerical derivatives in Eq. (A15) of Hu et al. (2001).
Thus for moderate variations from a `fiducial' model, the CMB peak
multipole number scales approximately as
 peak
peak

 m-0.14 h-0.48,
i.e. the condition for constant CMB peak location is well approximated as
m-0.14 h-0.48,
i.e. the condition for constant CMB peak location is well approximated as
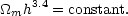 |
(156) |
However, information about the
peak heights does alter this degeneracy slightly; the relative peak
heights are preserved at constant
 m, hence
the actual likelihood ridge is a `compromise' between constant peak
location (constant
m, hence
the actual likelihood ridge is a `compromise' between constant peak
location (constant
 m
h3.4) and constant relative heights (constant
m
h3.4) and constant relative heights (constant
 m
h2); the peak locations have more weight in this
compromise, leading to a likelihood ridge along approximately
m
h2); the peak locations have more weight in this
compromise, leading to a likelihood ridge along approximately
 m
h3.0
m
h3.0  const
(Percival et al. 2002).
It is now clear how LSS data combines with the CMB:
const
(Percival et al. 2002).
It is now clear how LSS data combines with the CMB:
 m
h3.4
is measured to very high accuracy already, and Percival et al. deduced
m
h3.4
is measured to very high accuracy already, and Percival et al. deduced
 m
h3.4 = 0.078 with an error of
about 6% using pre-WMAP CMB data. The first-year WMAP results
in fact prefer
m
h3.4 = 0.078 with an error of
about 6% using pre-WMAP CMB data. The first-year WMAP results
in fact prefer
 m
h3.4 = 0.084
(Spergel et al. 2003);
the slight
increase arises because WMAP indicates that previous datasets around
the peak were on average calibrated low.
m
h3.4 = 0.084
(Spergel et al. 2003);
the slight
increase arises because WMAP indicates that previous datasets around
the peak were on average calibrated low.