The 2dFGRS power spectrum contains important information about the key parameters of the cosmological model, but we have seen that additional assumptions are needed, in particular the values of n and h. Observations of CMB anisotropies can in principle measure most of the cosmological parameters, and combination with the 2dFGRS can lift most of the degeneracies inherent in the CMB-only analysis. It is therefore of interest to see what emerges from a joint analysis.
The clearest immediate result is that the geometrical
degeneracy becomes broken
(Efstathiou et al. 2002).
A 95% confidence upper limit on any curvature can be set at
|
- 1| < 0.05.
We can therefore be confident
that the universe is very nearly flat
so it is defensible to assume
hereafter that this is exactly true. The importance of tensors
will of course be one of the key questions for cosmology over the
next several years, but it is interesting to consider the limit
in which these are negligible. In this case, the standard model
for structure formation contains a vector of only 6 parameters:
 |
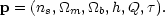(157) |
Of these, the optical depth to last scattering,
, is almost entirely
degenerate with the normalization, Q - and indeed with
the bias parameter; we discuss this below.
The remaining four parameters are pinned down very precisely:
using a compilation of pre-WMAP CMB data plus the 2dFRGS power spectrum,
Percival et al. (2002)
obtained
 |
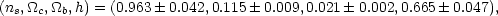(158) |
or an overall density parameter of
m = 0.313
± 0.055.
It is remarkable how well these figures agree with completely
independent determinations:
h = 0.72 ± 0.08 from the HST key project
(Mould et al. 2000;
Freedman et al. 2001);
b
h2 = 0.020± 0.001
(Burles et al. 2001).
This gives confidence that the tensor component must
indeed be sub-dominant.
This analysis was published in
Percival et al. (2002),
and is based on the preliminary version of the 2dFGRS power
spectrum, from
Percival et al. (2001).
We can make a first estimate of how this is likely to change using the
m
h = 0.18± 0.02 from the preliminary analysis
of P(k) from the final dataset. In combination with
the WMAP
m
h3.4 = 0.084 from the CMB peak degeneracy, this yields
 |
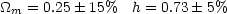(159) |
as the preferred current figures from an analysis of this type.
The matter density remains frustratingly imprecise, and
it is clear that it will be very hard to measure h accurately
enough to cure this problem. However, complementary constraints
on m
exist at similar precision (e.g.
m = 0.28
± 18% for a flat model from the SNe Ia Hubble diagram;
Tonry et al. 2003).
With new results from gravitational lensing,
m should
be measured to better than 10% precision within a year.
Perhaps the most striking conclusion from these results concerns
the nature of the primordial fluctuations, which remain
consistent with the n = 1 scale-invariant form. The WMAP
analysis of
Spergel et al. (2003)
yields 0.97 ± 0.03 from CMB plus 2dFGRS (cf. 0.96 ± 0.04 from
Percival et al. 2002).
The WMAP team also consider adding data from the
Lyman-
forest, which pushes the solution away from a pure power-law:
 |
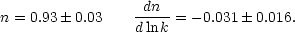(160) |
This evidence for running of n is at best marginal, and
disappears completely when systematic uncertainties in the
Lyman- data are considered
(Seljak, McDonald &
Makarov 2003).
It would in any case be surprising if true, since simple inflation
models suggest that
dn / d ln k should be second order in (n - 1).
Although the tensor degeneracy prevents any very strong statements,
the data are best described by pure scalar fluctuations, and
Percival et al. (2002)
set an upper limit of 0.7 to the tensor-to-scalar ratio.
The agreement with pure scalar n = 1 is not yet a strong
embarrassment for inflation, but it is starting to bite on
some inflationary models.
Leach & Liddle (2003)
show that CMB plus 2dFGRS are inconsistent with the
V = 
4
model at just about 95% confidence. It is possible to set up inflation
models in which tilt and tensors are both negligible, but there has been
a long-standing hope for more substantial signs of inflationary
dynamics; if these are not seen soon, it will be a major disappointment.