2.2. Dynamics: The Friedmann Equations

As mentioned, the RW metric is a purely kinematic consequence of requiring homogeneity and isotropy of our spatial sections. We next turn to dynamics, in the form of differential equations governing the evolution of the scale factor a(t). These will come from applying Einstein's equation,

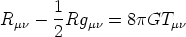(13)

to the RW metric.

Before diving right in, it is useful to consider the types of energy-momentum tensors T_µ we will typically encounter in cosmology. For simplicity, and because it is consistent with much we have observed about the universe, it is often useful to adopt the perfect fluid form for the energy-momentum tensor of cosmological matter. This form is

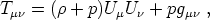(14)

where U^µ is the fluid four-velocity, is the energy density in the rest frame of the fluid and p is the pressure in that same frame. The pressure is necessarily isotropic, for consistency with the RW metric. Similarly, fluid elements will be comoving in the cosmological rest frame, so that the normalized four-velocity in the coordinates of (7) will be

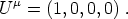(15)

The energy-momentum tensor thus takes the form

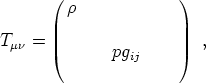(16)

where g_ij represents the spatial metric (including the factor of a²).

Armed with this simplified description for matter, we are now ready to apply Einstein's equation (13) to cosmology. Using (7) and (14), one obtains two equations. The first is known as the Friedmann equation,

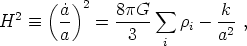(17)

where an overdot denotes a derivative with respect to cosmic time t and i indexes all different possible types of energy in the universe. This equation is a constraint equation, in the sense that we are not allowed to freely specify the time derivative ; it is determined in terms of the energy density and curvature. The second equation, which is an evolution equation, is

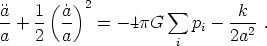(18)

It is often useful to combine (17) and (18) to obtain the acceleration equation

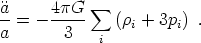(19)

In fact, if we know the magnitudes and evolutions of the different energy density components _i, the Friedmann equation (17) is sufficient to solve for the evolution uniquely. The acceleration equation is conceptually useful, but rarely invoked in calculations.

The Friedmann equation relates the rate of increase of the scale factor, as encoded by the Hubble parameter, to the total energy density of all matter in the universe. We may use the Friedmann equation to define, at any given time, a critical energy density,

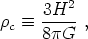(20)

for which the spatial sections must be precisely flat (k = 0). We then define the density parameter

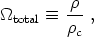(21)

which allows us to relate the total energy density in the universe to its local geometry via

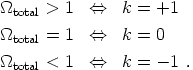(22)

It is often convenient to define the fractions of the critical energy density in each different component by

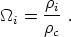(23)

Energy conservation is expressed in GR by the vanishing of the covariant divergence of the energy-momentum tensor,

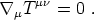(24)

Applying this to our assumptions - the RW metric (7) and perfect-fluid energy-momentum tensor (14) - yields a single energy-conservation equation,

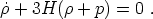(25)

This equation is actually not independent of the Friedmann and acceleration equations, but is required for consistency. It implies that the expansion of the universe (as specified by H) can lead to local changes in the energy density. Note that there is no notion of conservation of "total energy," as energy can be interchanged between matter and the spacetime geometry.

One final piece of information is required before we can think about solving our cosmological equations: how the pressure and energy density are related to each other. Within the fluid approximation used here, we may assume that the pressure is a single-valued function of the energy density p = p(). It is often convenient to define an equation of state parameter, w, by

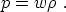(26)

This should be thought of as the instantaneous definition of the parameter w; it need represent the full equation of state, which would be required to calculate the behavior of fluctuations. Nevertheless, many useful cosmological matter sources do obey this relation with a constant value of w. For example, w = 0 corresponds to pressureless matter, or dust - any collection of massive non-relativistic particles would qualify. Similarly, w = 1/3 corresponds to a gas of radiation, whether it be actual photons or other highly relativistic species.

A constant w leads to a great simplification in solving our equations. In particular, using (25), we see that the energy density evolves with the scale factor according to

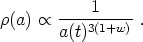(27)

Note that the behaviors of dust (w = 0) and radiation (w = 1/3) are consistent with what we would have obtained by more heuristic reasoning. Consider a fixed comoving volume of the universe - i.e. a volume specified by fixed values of the coordinates, from which one may obtain the physical volume at a given time t by multiplying by a(t)³. Given a fixed number of dust particles (of mass m) within this comoving volume, the energy density will then scale just as the physical volume, i.e. as a(t)^-3, in agreement with (27), with w = 0.

To make a similar argument for radiation, first note that the expansion of the universe (the increase of a(t) with time) results in a shift to longer wavelength , or a redshift, of photons propagating in this background. A photon emitted with wavelength _e at a time t_e, at which the scale factor is a_e a(t_e) is observed today (t = t₀, with scale factor a₀ a(t₀)) at wavelength _o, obeying

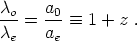(28)

The redshift z is often used in place of the scale factor. Because of the redshift, the energy density in a fixed number of photons in a fixed comoving volume drops with the physical volume (as for dust) and by an extra factor of the scale factor as the expansion of the universe stretches the wavelengths of light. Thus, the energy density of radiation will scale as a(t)^-4, once again in agreement with (27), with w = 1/3.

Thus far, we have not included a cosmological constant in the gravitational equations. This is because it is equivalent to treat any cosmological constant as a component of the energy density in the universe. In fact, adding a cosmological constant to Einstein's equation is equivalent to including an energy-momentum tensor of the form

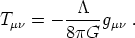(29)

This is simply a perfect fluid with energy-momentum tensor (14) with

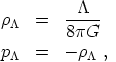(30)

so that the equation-of-state parameter is

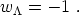(31)

This implies that the energy density is constant,

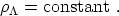(32)

Thus, this energy is constant throughout spacetime; we say that the cosmological constant is equivalent to vacuum energy.

Similarly, it is sometimes useful to think of any nonzero spatial curvature as yet another component of the cosmological energy budget, obeying

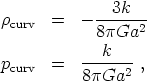(33)

so that

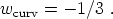(34)

It is not an energy density, of course; _curv is simply a convenient way to keep track of how much energy density is lacking, in comparison to a flat universe.