2.4. Including Curvature

It is true that we know observationally that the universe today is flat to a high degree of accuracy. However, it is instructive, and useful when considering early cosmology, to consider how the solutions we have already identified change when curvature is included. Since we include this mainly for illustration we will focus on the separate cases of dust-filled and radiation-filled FRW models with zero cosmological constant. This calculation is an example of one that is made much easier by working in terms of conformal time .

Let us first consider models in which the energy density is dominated by matter (w = 0). In terms of conformal time the Einstein equations become

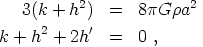(38)

where a prime denotes a derivative with respect to conformal time and h() a' / a. These equations are then easily solved for h() giving

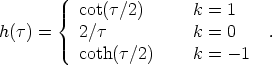(39)

This then yields

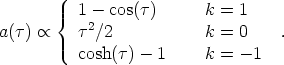(40)

One may use this to derive the connection between cosmic time and conformal time, which here is

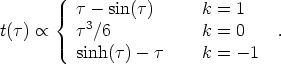(41)

Next we consider models dominated by radiation (w = 1/3). In terms of conformal time the Einstein equations become

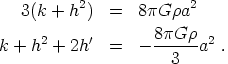(42)

Solving as we did above yields

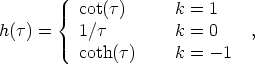(43)

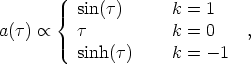(44)

and

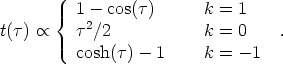(45)

It is straightforward to interpret these solutions by examining the behavior of the scale factor a(); the qualitative features are the same for matter- or radiation-domination. In both cases, the universes with positive curvature (k = + 1) expand from an initial singularity with a = 0, and later recollapse again. The initial singularity is the Big Bang, while the final singularity is sometimes called the Big Crunch. The universes with zero or negative curvature begin at the Big Bang and expand forever. This behavior is not inevitable, however; we will see below how it can be altered by the presence of vacuum energy.