In the previous lecture we set up the tools required to analyze the kinematics and dynamics of homogeneous and isotropic cosmologies in general relativity. In this lecture we turn to the actual universe in which we live, and discuss the remarkable properties cosmologists have discovered in the last ten years. Most remarkable among them is the fact that the universe is dominated by a uniformly-distributed and slowly-varying source of "dark energy," which may be a vacuum energy (cosmological constant), a dynamical field, or something even more dramatic.
3.1. Matter: Ordinary and Dark
In the years before we knew that dark energy was an important
constituent of the universe, and before observations of
galaxy distributions and CMB anisotropies
had revolutionized the study of structure in the universe, observational
cosmology sought to measure two numbers: the Hubble constant
H0 and the matter density parameter
M. Both of
these quantities remain undeniably important, even though we have
greatly broadened the scope of what we hope to measure. The Hubble
constant is often parameterized in terms of a dimensionless
quantity h as
 |
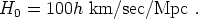(52) |
After years of effort, determinations of this number seem to have zeroed in on a largely agreed-upon value; the Hubble Space Telescope Key Project on the extragalactic distance scale [21] finds
 |
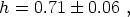(53) |
which is consistent with other methods [22], and what we will assume henceforth.
For years, determinations of
M based
on dynamics
of galaxies and clusters have yielded values between approximately
0.1 and 0.4, noticeably smaller than the critical density.
The last several years have witnessed a number of new methods
being brought to bear on the question; here we sketch some of
the most important ones.
The traditional method to estimate
the mass density of the universe is to "weigh" a cluster of
galaxies, divide by its luminosity, and extrapolate the
result to the universe as a whole. Although clusters are not
representative samples of the universe, they are sufficiently
large that such a procedure has a chance of working. Studies
applying the virial theorem to cluster dynamics have typically
obtained values
M = 0.2
± 0.1
[23,
24,
25].
Although it is possible that
the global value of M/L differs appreciably from its value
in clusters, extrapolations from small scales do not seem
to reach the critical density
[26]. New
techniques to weigh the clusters, including gravitational
lensing of background galaxies
[27] and temperature
profiles of the X-ray gas
[28],
while not yet in perfect agreement with each other, reach essentially
similar conclusions.
Rather than measuring the mass relative to the luminosity
density, which may be different inside and outside clusters,
we can also measure it with respect to the baryon density
[29],
which is very likely to have the same value in clusters as
elsewhere in the universe, simply because there is no way
to segregate the baryons from the dark matter on such large
scales. Most of the baryonic mass is in the hot intracluster gas
[30],
and the fraction fgas
of total mass in this form can be measured either by
direct observation of X-rays from the gas
[31]
or by distortions of the microwave background by scattering off hot
electrons (the Sunyaev-Zeldovich effect)
[32],
typically yielding
0.1 
fgas
0.2.
Since primordial nucleosynthesis provides a determination of
B ~ 0.04,
these measurements imply
 |
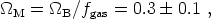(54) |
consistent with the value determined from mass to light ratios.
Another handle on the density parameter in matter comes from
properties of clusters at high redshift. The very existence
of massive clusters has been used to argue in favor of
M ~ 0.2
[33],
and the lack of appreciable
evolution of clusters from high redshifts to the present
[34,
35]
provides additional evidence that
M <
1.0. On the other hand, a recent measurement
of the relationship between the temperature and luminosity of
X-ray clusters measured with the XMM-Newton satellite
[36]
has been interpreted as evidence for
M near
unity. This last result seems at odds with a
variety of other determinations, so we should keep a careful watch
for further developments in this kind of study.
The story of large-scale motions is more ambiguous. The
peculiar velocities of galaxies are sensitive to the underlying
mass density, and thus to
M, but
also to the "bias" describing the relative amplitude of fluctuations in
galaxies and mass
[24,
37]. Nevertheless,
recent advances in very large redshift surveys have led to
relatively firm determinations of the mass density; the 2df
survey, for example, finds
0.1
M
0.4
[38].
Finally, the matter density parameter can be extracted from
measurements of the power spectrum of density fluctuations
(see for example
[39]).
As with the CMB, predicting
the power spectrum requires both an assumption of the correct
theory and a specification of a number of cosmological
parameters. In simple models (e.g., with only cold dark
matter and baryons, no massive neutrinos), the spectrum can be
fit (once the amplitude is normalized) by a single "shape
parameter", which is found to be equal to
=
M
h. (For more complicated models see
[40].)
Observations then yield
~ 0.25,
or M ~
0.36. For a more careful comparison
between models and observations, see
[41,
42,
43,
44].
Thus, we have a remarkable convergence on values for the density parameter in matter:
 |
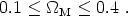(55) |
As we will see below, this value is in excellent agreement with that which we would determine indirectly from combinations of other measurements.
As you are undoubtedly aware, however, matter comes in different forms; the matter we infer from its gravitational influence need not be the same kind of ordinary matter we are familiar with from our experience on Earth. By "ordinary matter" we mean anything made from atoms and their constituents (protons, neutrons, and electrons); this would include all of the stars, planets, gas and dust in the universe, immediately visible or otherwise. Occasionally such matter is referred to as "baryonic matter", where "baryons" include protons, neutrons, and related particles (strongly interacting particles carrying a conserved quantum number known as "baryon number"). Of course electrons are conceptually an important part of ordinary matter, but by mass they are negligible compared to protons and neutrons; the mass of ordinary matter comes overwhelmingly from baryons.
Ordinary baryonic matter, it turns out, is not nearly enough to account for the observed matter density. Our current best estimates for the baryon density [45, 46] yield
 |
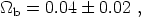(56) |
where these error bars are conservative by most standards. This determination comes from a variety of methods: direct counting of baryons (the least precise method), consistency with the CMB power spectrum (discussed later in this lecture), and agreement with the predictions of the abundances of light elements for Big-Bang nucleosynthesis (discussed in the next lecture). Most of the matter density must therefore be in the form of non-baryonic dark matter, which we will abbreviate to simply "dark matter". (Baryons can be dark, but it is increasingly common to reserve the terminology for the non-baryonic component.) Essentially every known particle in the Standard Model of particle physics has been ruled out as a candidate for this dark matter. One of the few things we know about the dark matter is that is must be "cold" - not only is it non-relativistic today, but it must have been that way for a very long time. If the dark matter were "hot", it would have free-streamed out of overdense regions, suppressing the formation of galaxies. The other thing we know about cold dark matter (CDM) is that it should interact very weakly with ordinary matter, so as to have escaped detection thus far. In the next lecture we will discuss some currently popular candidates for cold dark matter.